Parameters of substructure in wrought Cu – Mn alloys with FCC lattice

Introduction

Variation in the composition of alloys of Cu – Mn system can change the degree of short-range order and the resistance to motion of dislocations [1, 2]. At the same time, in the alloys of this system, the value of the stacking-fault energy (SFE) slightly depends on the concentration of the alloying element – manganese [3]. Variation in the concentration of the second element in the solid solution can lead to a change in the dislocation start stress and friction forces and, consequently, to a change in the resistance to the beginning of plastic deformation. An increase in the deformation degree leads to formation of a certain type of dislocation substructure, which, in turn, determines the deformation hardening of polycrystals. The nature and type of the dislocation structures formed are closely connected with the SFE value, local order parameters, and friction forces between dislocations. These parameters can significantly vary depending on the concentration of the alloying element, degree of ordering in solid solutions, as well as deformation degree [4 – 6].

For many years, the dislocation structure was characterized mainly by such a parameter as the mean scalar density of dislocations <ρ>. Further development of the dislocation study has led to the division of <ρ> into the following components which have different physical meanings: geometrically necessary (ρ_G) and statisticallystored (ρ_S) dislocations. The references show thatthe geometrically necessary dislocations are formedin the case of deformations in the polycrystal metals and alloys with deformation twins, in the dispersion-hardened materials and in other cases of functioning of strong barriers to dislocation sliding [7 – 9].

Density ρ_G is directly connected with the curvature-torsion of the crystal lattice χ [13, 14]:

\[{\rho _G} = \frac{1}{b}\frac{{\partial \varphi }}{{\partial \ell }} = \frac{\chi }{b} = {(rb)^{ - 1}},\]

where b is the Burgers vector; φ is the tilting angle of the crystal plane; ℓ is the distance on the plane; \(\chi  = \large\frac{{\partial \varphi}}{{\partial \ell}}\) is the curvature-torsion of the crystal lattice; r is the radius of crystal curvature.

The formation of dislocations and dislocation reactions in the alloys after plastic deformation can be considered to be random processes. The dislocations subjected to deceleration by others formed in the course of plastic deformation are called statistically stored dislocations (SSD) [11]. Such statistically stored dislocations are formed at the very beginning of plastic deformation and are decelerated mainly by weak barriers consisting of other dislocations. When the stronger barriers (such as particles of second phases, deformation twins, or grain boundaries) are present in the alloys, the geometrically necessary dislocations (GND) accumulate in the material, and plastic deformation gradients (1) are available [11]. As a result, the mean scalar density of dislocations is determined by the following equation

<ρ> = ρ_S + ρ_G.

This work studies the influence of manganese alloying and grain size in wrought Cu – Mn alloys with FCC lattice using the transmission electron microscopy.

Study materials and methods

The study materials are polycrystal alloys of Cu – Mn system in the manganese concentration range from 0.4 to 25 % (henceforward, atomic (at.) percentage). Alloys with the mean grain size of 10, 20, 40, 60, 100, 120 and 240 µm were studied. Samples of the alloys studied were deformed by elongation at the room temperature with a rate of 2·10^–2 s^–1. The dislocation structure was studied by menans of transmission diffraction electron microscopy (TEM) using goniometer-equipped electron microscopes with accelerating voltage of 125 kV. The foils were examined in the microscope column at a 30,000-power magnification. The technique for measuring the dislocation structure parameters is given in [12, 13].

Results and discussion

We considered formation of the dislocation substructure (DSS) depending on the concentration of the alloying element at small (ε_tr = 0.05) deformation degrees in the copper-manganese alloys. For easy comparison of the substructures, the study results are provided for one grain size equal to 100 µm.

Fig. 1 shows the types of the dislocation substructures formed with growth of the second element. Analysis of the electron microscope images allowed us to find the following regularities in the DSS formations. With the moderate deformation degrees (ε_tr = 0.05 – 0.10) in the alloys studied (Cu + 0.4 % Mn, Cu + 8 % Mn and Cu + 19 % Mn), tangles (Fig. 1, a) as well as cell substructures without disorientations (Fig. 1, b) are formed from the dislocations. The increase in the concentration of the second component up to 8 % Mn results in transition from the cell DSS to the cell-mesh DSS (Fig. 1, c). The further growth of the second element concentration is accompanied by the formation of the new DSS type. In alloys Cu + 13 % Mn, Cu + 19 % Mn and Cu + 25 % Mn, we can observe the following sequence of the DSS types formation: dislocation chaos (Fig. 1, d); dislocation clusters and dislocation loops (Fig. 1, e); mesh DSS (Fig. 1, f ) respectively.

We considered the influence of the deformation degree growth in the alloys studied, resulting in disorientations appeared in the DSS. The electron microscope images show this process as the appearance of the extinction deformation contours (Fig. 2).

In Cu – Mn alloys with a low concentration of the alloying element (up to 6 %), the disoriented cell substructure is formed with the deformation degree of 0.20 (Fig. 2, a). In alloys with a concentration of the alloying element higher than 8 % Mn, the disoriented cell-mesh substructure develops with further deformation increase (Fig. 2, b). With such deformation, clumps are formed from dislocations (Fig. 2, b) which riginate on the long rectilinear dislocations formed even at low deformation degrees. As a result, an increase in the density of clumps is observed, and the structure tends to become more homogeneous.

Fig. 2 provides electron microscope images of the DSS types formed with the higher deformation degrees (ε_tr > 0.20) in the alloys with different concentrations of the alloying element. The experiments established that, in the alloys with concentration of the second element equal to 0.4, 2.4 and 6 % Mn, the following substructures are observed: disoriented cell, cell-mesh, and microstrip DSS. The examples of the substructure types observed for alloy Cu + 0.4 % Mn are provided in Fig. 2, a and b. In alloy Cu + 6 % Mn, the formation of the microstrip DSS is observed inside the grain, appearing along boundaries of the disoriented cells or from the grain boundaries (Fig. 2, c). It is important to note that the kinetics of the microstrip substructure formation and volume fraction growth is often connected with growth through the alloy of the broken boundaries.

It was established that, in alloys with the higher concentration of the alloying element (8, 10, 13, 19 and 25 % Mn), such substructures as disoriented mesh, disoriented cell-mesh, and microstrip DSS are present The example of the substructures observed at ε_tr > 0.20 is shown in Fig. 2, d – f for alloy Cu + 19 % Mn. Based on the analysis of the electron microscope photos, it was established that the alloy with 8 % Mn is the boundarywhen transferring from the classically cell DSS to cell-mesh DSS.

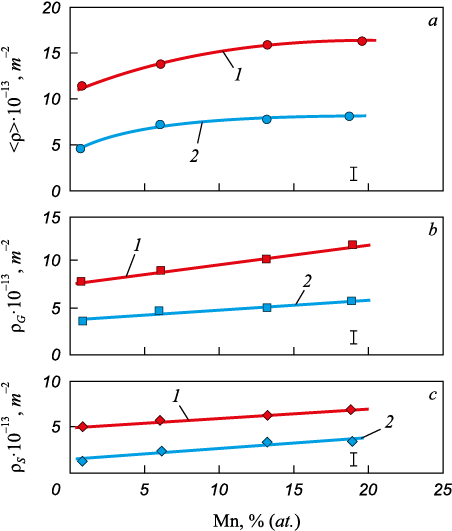
The photographs were used to measure the mean scalar density of dislocations <ρ>, the density of statistically stored (ρ_S) and geometrically necessary (ρ_G) dislocations, the curvature-torsion of the crystalline lattice χ, the density of microstrips P_strip, as well as the density of broken boundaries Mbr.bndwith different grain sizes <d>. The dependencies of the mean scalar density of dislocations, density of geometrically necessary and statistically stored dislocations on the concentration of alloying element C_Mn at ε_tr = 0.30 and grain sizes 10 and 240 μm are provided in Fig. 3.

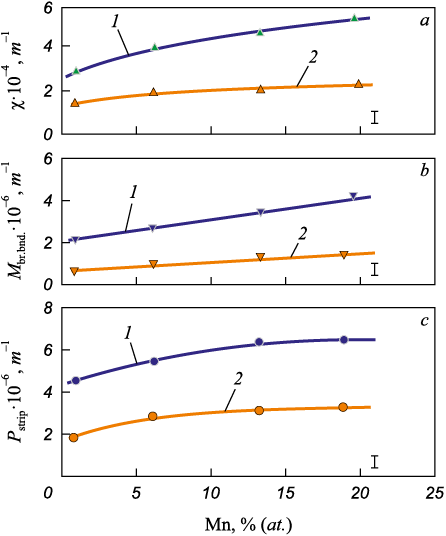
The growth of manganese concentration results in increase of both mean scalar density of dislocations <ρ> and its components ρ_G and ρ_S. The growth of deformation degree results in formation of disorientations in the substructure. Fig. 4 shows dependencies of the parameters which characterized is orientations in Cu – Mn alloys: the curvature-torsion of the crystal lattice, the density of microstrips, and the density of broken sub-boundaries. The values of χ, P_strip, and M_br. bnd. increase with the increase of the concentration of the alloying element C_Mn more significantly in the alloys with the grain size of 10 µm compared to the alloys with the grain size of 240 µm.

We considered the features of the atomic volume change in solid solutions in the alloys of Cu – Mn system. It is believed that, in the range of existence of solid solutions of two elements, the change in the lattice period depending on the composition should be linear. This assumption was represented as the Vegard’s law [14 – 16]. According to this law, the lattice period of the solid solution of two components with the same or similar structure and periods a₁ and a₂ should change linearly depending on the concentration of these components x₁ and x₂ expressed in atomic fractions:

а = x₁a₁ + x₂a₂.

On the other hand, Zen proposed the atomic volume additivity rule for ideal solid solutions [15–17]:

Ω = С_АΩ_А + С_ВΩ_В,

where С_А and С_В, Ω_А и Ω_В are the concentrations and atomic volumes of the pure components.

A volume fraction of the elementary cell per one atom is understood as the atomic volume, that is:

where n is the number of atoms in the elementary cell.

Atomic volumes of pure metals Ω calculated in this way depend least of all on the crystal lattice type. The atomic volume of pure metals Ω is the more universal characteristic with respect to the parameters of elementary cell parameters pure metals and can be used to analyze the properties of compounds formed by elements with different crystal structures. This approach was successfully applied in [14] during analysis of Ti-Ni-based binary compounds.

Zen’s law is true just as rare as Vegard’s rule; however, it is very popular. There are many models for predicting deviations from the Zen’s law, but the reliability level of these predictions is low. None of the models predicts even a deviation sign with an accuracy of more than 60 %. This suggests that the main factors of the deviation from Zen’s law have not yet been identified.

For the most of the known alloys where solid solutions are formed, the negative deviation of the atomic volume from Zen’s rule is observed [18, 17]:

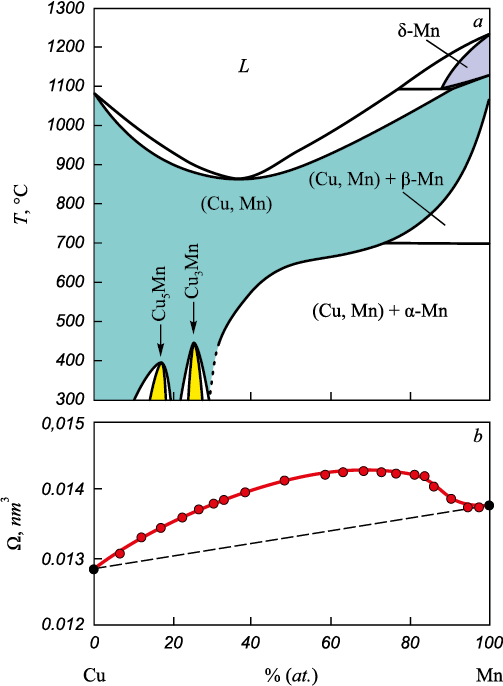
Fig. 5, a shows a phase diagram of Cu – Mn system with two concentration areas where ordered phases are formed as a result of “disorder – order” phase transitions of compositions Cu₅Mn and Cu₃Mn, as well as concentration dependencies of atomic volumes of the alloys of system Cu – Mn (Fig. 5, b). Within the alloys of this system, the positive deviation of the atomic volume from the Zen’s law is observed. Such deviation from the Zen’s law on the concentration dependency of the atomic volume occurs much less frequently than the negative deviation [20].

The above data indicates a change in the forces of interatomic interaction during formation of solid solutions in Cu – Mn system (according to equation connecting the crystal energy and atomic volume Ω in the case of metal nature of atomic interaction [21]):

\[U = \frac{{A{e^2}}}{{{\Omega ^{1/3}}}} + \frac{B}{{{\Omega ^{2/3}}}} + \frac{{C{e^2}}}{\Omega };\]

where \(\large\frac{{A{e^2}}}{{{\Omega ^{1/3}}}}\) and \(\large\frac{B}{{{\Omega ^{2/3}}}}\) are the potential and kinetic energies of free electrons; \(\large\frac{{C{e^2}}}{\Omega }\) characterizes the kinetic energy of electrons which occupy the lower energy states.

It is known that Peierls stress E_P, which is the minimum required stress for dislocation displacementin crystal bodies, depends on the interplane distance d. In this case, maximum E_P, that is the Peierls barrier value is determined as follows [22]

\[{\tau _P} = \frac{G}{{1 - \nu}}\exp \left( { - \frac{{2\pi{\omega _{\rm{d}}}}}{b}}\right),\]

where \({\omega _{\rm{d}}} = \large\frac{d}{{1 - \nu}}\) is the dislocation width; d is the interplane distance; G is the shear modulus; ν is the Poisson’s ration; b is the Burgers vector.

Thus, the dependence of the atomic volume on the concentration for the alloys of Cu – Mn system allows us to state, according to the above analysis based on equations (1) and (2), that the increase in atomic volume contributes to the crystal energy change and the Peierls barrier height. Such changes in the atomic volume exercise significant influence over mobility of the statistically stored and geometrically necessary dislocations.

Conclusions

Based on the electron microscope study of the fine structure of wrought samples of the alloys of Cu – Mn system with FCC lattice, the parameters of the dislocation substructures are determined (mean scalar density of dislocations <ρ> and its components: density of statistically stored ρ_S and geometrically necessary ρ_G dislocations; curvature-torsion of crystal lattice χ, density of microstrips P_strip and density of broken sub-boundaries M_br. bnd.) depending on the concentration of alloying element (manganese) with different grain sizes. Features of evolution of the dislocation substructures in alloys with different manganese content are determined; and it is established that the alloy with 8 % Mn is the boundary when transferring from the classically cell DSS to cell-mesh DSS.

It was shown that the grain size decrease results in dislocation structure parameters increase. This is due to the fact that dislocation accumulation in the grains of smaller size is connected with their lower mobility.

Based on the analysis of concentration dependences of the atomic volumes in the alloys of Cu – Mn system, the positive deviation from Zen’s law was established. Such an increase in atomic volume with the alloying element concentration growth contributes to the crystal energy change and, as a result, to the Peierls barrier increase. This xercises significant influence over mobility of the statistically stored and geometrically necessary dislocations. This data correlates with the results of electron microscope studies: in Cu – Mn alloys with the higher manganese content, the dislocation substructure parameters growth is observed.

It was also established that the grain size decrease has more significant effect on the dislocation substructure parameters than does the content of alloying element atoms in the alloys of Cu – Mn system with FCC lattice.