Перейти к:
Энергия и скорость скольжения краевой и винтовой дислокаций в аустените и стали Гадфильда: молекулярно-динамическое моделирование
https://doi.org/10.17073/0368-0797-2022-12-861-868
Аннотация
Методом молекулярной динамики проведено исследование скольжения краевой и винтовой дислокаций в стали Гадфильда и в чистом ГЦК железе (аустените) в зависимости от температуры и скорости деформирования. Полная дислокация появляется в настоящей модели сразу в виде расщепленной на пару частичных дислокаций Шокли, разделенных дефектом упаковки. Расстояние между частичными дислокациями составляет несколько нанометров. При увеличении скорости сдвига это расстояние уменьшается. Согласно полученным данным энергии краевой и винтовой дислокаций в стали выше, чем в чистом аустените. Энергия полной краевой дислокации в γ-железе и в стали Гадфильда составляет в среднем 2,0 и 2,3 эВ/Å, винтовой – 1,3 и 1,5 эВ/Å соответственно. Получены зависимости скорости скольжения краевой и винтовой дислокаций в зависимости от скорости сдвига и температуры. Скорость скольжения краевой дислокации во всех случаях выше, чем винтовой, что объясняется отличием скорости распространения продольной и поперечной волн в материале. С ростом скорости сдвига скорость скольжения возрастает до определенного предела, зависящего от скорости распространения соответствующих упругих волн. При низких и нормальных температурах скорость скольжения дислокаций в стали Гадфильда существенно (примерно в полтора раза) ниже по сравнению с чистым ГЦК железом. В чистом железе с ростом температуры скорость скольжения дислокаций уменьшается. Однако для стали Гадфильда эта зависимость немонотонна: по мере увеличения температуры примерно до 500 К скорость дислокаций возрастает (что связано связано, по всей видимости, с интенсификацией диффузии примесных атомов углерода), а затем, как и в железе, падает.
Для цитирования:
Зоря И.В., Полетаев Г.М., Ракитин Р.Ю. Энергия и скорость скольжения краевой и винтовой дислокаций в аустените и стали Гадфильда: молекулярно-динамическое моделирование. Известия высших учебных заведений. Черная Металлургия. 2022;65(12):861-868. https://doi.org/10.17073/0368-0797-2022-12-861-868
For citation:
Zorya I.V., Poletaev G.M., Rakitin R.Yu. Energy and velocity of sliding of edge and screw dislocations in austenite and Hadfield steel: Molecular dynamics simulation. Izvestiya. Ferrous Metallurgy. 2022;65(12):861-868. (In Russ.) https://doi.org/10.17073/0368-0797-2022-12-861-868
Введение
Образованию и скольжению дислокаций в металлах и сплавах посвящено много работ, в том числе выполненных с помощью компьютерного моделирования [1 – 5]. Помимо сложных вопросов взаимодействия дислокаций друг с другом и с различными дефектами внимание в современных работах обращено и на относительно простые вопросы, например, зависимость скорости скольжения дислокации от температуры и скорости деформирования [3, 6]. С ростом скорости деформирования скорость дислокаций, как известно, сначала растет, а затем достигает некоторого предела, который, как правило, меньше скорости звука в данном материале. Причем разные авторы приводят разные значения этого предела в отношении к скорости звука [3, 6 – 8]. С ростом температуры, как отмечает большинство исследователей, скорость скольжения дислокаций снижается [3, 6, 7]. В качестве причин этого снижения рассматривают фононное рассеяние, изменение модуля сдвига с температурой и т.д.
Настоящая работа посвящена исследованию с помощью метода молекулярной динамики скольжения краевой и винтовой дислокаций в стали Гадфильда и в γ-железе (аустените) в зависимости от температуры и скорости деформирования. Отдельное рассмотрение γ-железа связано со стремлением выделить роль примесей (марганца и углерода) в стали Гадфильда. Эта сталь благодаря ее превосходной способности к деформационному упрочнению [9, 10] имеет большое практическое значение и долгую историю исследования уникальных свойств. Вместе с тем на сегодняшний день существует очень мало работ, посвященных моделированию ее атомной структуры и процессов, происходящих в ней в условиях деформации, на атомном уровне, что обусловлено, в частности, сложностью моделирования подобных многокомпонентных систем. В настоящее время остается ряд вопросов, связанных с механизмами протекания пластической деформации на атомном уровне в сталях, которые возможно решить методами компьютерного моделирования. К таким вопросам относятся, например, особенности образования и распространения дислокаций в зависимости от различных факторов, механизмы взаимодействия друг с другом, границами зерен, двойниками и другими дефектами.
Описание модели
Сталь Гадфильда, как известно, является многокомпонентной системой и, помимо классических железа, марганца и углерода, может содержать массу других легирующих элементов [9, 10]. В настоящем исследовании ограничились системой, включающей три базовых элемента: γ-Fe в качестве матрицы, марганец и углерод. Для описания взаимодействий атомов железа друг с другом использовался ЕАМ потенциал Лау [11], хорошо воспроизводящий структурные, энергетические и упругие характеристики аустенита [11, 12]. Для всех остальных пяти межатомных взаимодействий в системе γ-Fe – Mn – C использовались потенциалы Морзе, найденные ранее в работе [13] на основе экспериментальных данных по энергии растворения и энергии миграции соответствующих примесных атомов в кристалле ГЦК железа, радиусу атомов, их электроотрицательности, энергии взаимной связи и другим характеристикам.
При моделировании атомной структуры стали Гадфильда использовалось стандартное соотношение компонентов: 13 % Mn и 1,2 % C (по массе) (или 12,63 % Mn и 5,33 % C (ат.)) [9, 10]. Атомы марганца вводили в ГЦК решетку железа случайным образом, замещая атомы железа. Энергия связи атомов марганца и углерода в решетке аустенита очень высокая ‒ порядка 0,35 эВ согласно данным работы [14], т.е. примерно того же порядка, что и энергия связи атомов углерода с вакансиями (0,37 – 0,41 эВ [15]). То есть атомы марганца являются своего рода эффективными «ловушками» для примесных атомов углерода, не позволяя, в частности, последним образовывать скопления на дислокациях и границах зерен. В связи с этим атомы углерода вводились в модели в ближайшие к атомам марганца октаэдрические пустоты ГЦК решетки. Выбор атомов марганца, рядом с которыми вводились атомы углерода, а также выбор одной из соседних с ними октаэдрических пустот, производились случайно.
В γ-железе, которое рассматривалось в настоящей работе для сравнения со сталью Гадфильда, на всем интервале варьирования температуры тип кристаллической решетки сохранялся постоянным, полиморфное превращение не учитывалось. Как уже говорилось выше, рассмотрение аустенита проводилось для определения вклада примесей марганца и углерода в изучаемых процессах. Шаг интегрирования по времени (согласно методу молекулярной динамики) составлял 2 фс [16 ‒ 18]. Температуру в модели задавали через начальные скорости атомов согласно распределению Максвелла. При задании температуры обязательным являлся учет теплового расширения кристаллической решетки. Для используемых в работе потенциалов межатомного взаимодействия предварительно были найдены усредненные коэффициенты теплового расширения в молекулярно-динамической модели: 18·10 –6 К–1 для γ-Fe и 16·10–6 К–1 для стали Гадфильда. Для сохранения температуры постоянной в процессе моделирования использовался термостат Нозе-Гувера.
В кристаллах с ГЦК решеткой преимущественной является система скольжения {111}<110> [7, 8]. Плоскости {111} – наиболее плотноупакованные, в этих же плоскостях образуются дефекты упаковки (ДУ). Вектор Бюргерса полной дислокации в этом случае 1/2<110>. Но такая дислокация, как правило, расщепляется на две частичные дислокации с векторами Бюргерса 1/6<112, между которыми формируется дефект упаковки.
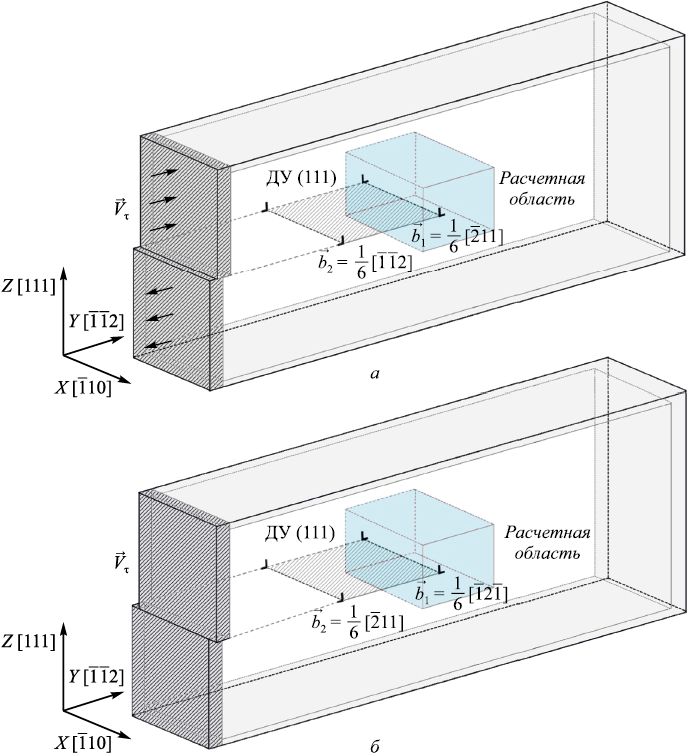
Для моделирования движущейся дислокации была создана прямоугольная расчетная ячейка, содержащая около 30 000 атомов (рис. 1), с ориентацией осей: X – [\(\bar 110\)], Y – [\(\bar 1\bar 12\)], Z – [111]. Плоскость XY в данном случае соответствует плоскости скольжения дислокации (111). Для инициации движения дислокации создавался сдвиг от торца расчетной ячейки. На рис. 1, a изображена схема создания движущейся полной краевой дислокации 1/2[\(\bar 101\)](111), а на рис. 1, б – винтовой дислокации 1/2[\(\bar 101\)](111). Темные заштрихованные области с левого торца перемещались как единое целое вдоль показанных направлений: в случае моделирования краевой дислокации верхняя часть торца смещалась вдоль плотноупакованного направления [\(\bar 101\)], нижняя – вдоль противоположного направления [\(10\bar 1\)] (рис. 1, a); в случае винтовой – вдоль направлений [\bar 110\)] (ось X) и [1\bar 10\)]. Атомы внутри темных заштрихованных областей в процессе компьютерного моделирования смещались только вдоль указанных направлений с задаваемой скоростью сдвига Vτ . Граничные условия с этой стороны, таким образом, были жесткими. Вдоль оси X, вдоль ядра дислокации, граничные условия задавались периодическими, то есть имитировалось бесконечное повторение структуры расчетной ячейки вдоль оси X. По другим границам использовали специальный тип граничных условий – условно жесткий: все атомы в серой области (сверху, снизу и справа на рис. 1) в процессе моделирования имели возможность двигаться только вдоль плоскости XY, движение вдоль оси Z исключалось. Этого было достаточно для удержания, с одной стороны, заданной прямоугольной формы расчетной ячейки и, с другой стороны, свободного выхода дислокаций за ее пределы.
Рис. 1. Модель краевой (а) и винтовой (б) дислокаций |
Скорость сдвига Vτ оставалась постоянной в течение компьютерного эксперимента. В некоторый момент времени сдвиг в левой части расчетной ячейки провоцировал появление дислокации: краевой или винтовой в зависимости от направления сдвига. Полная дислокация появлялась сразу в виде расщепленной на пару частичных дислокаций Шокли, разделенных дефектом упаковки в плоскости (111). Для краевой дислокации реакция расщепления имела вид 1/2 [\(\bar 101\)] → 1/6 [\(\bar 211\)] + 1/6 [ \(\bar 1\bar 12\)], для винтовой – 1/2 [\(\bar 110\)] → 1/6 [\(\bar 12\bar 1\)] + 1/6 [\(\bar 211\)]. Расстояние между частичными дислокациями определяется, как известно, энергией дефекта упаковки. В настоящей работе оно составляло несколько нанометров (в зависимости от скорости сдвига), что согласуется с результатами моделирования других авторов, например, в работах [3 – 5].
Результаты и обсуждение
Для расчета энергии дислокации в расчетной ячейке выбиралась расчетная область (выделена голубым на рис. 1). В процессе движения дислокации и прохождения ее через расчетную область вычисляли разность начальной и текущей потенциальной энергий атомов в области, деленной на ширину расчетной ячейки вдоль оси X, то есть на длину ядра дислокации. Размер расчетной области вдоль оси Y подбирали таким, чтобы он, с одной стороны, был больше расстояния между частичными дислокациями (чтобы в расчетной области мог одновременно поместиться весь комплекс из двух частичных дислокаций) и, с другой, не такой большой, чтобы в нее могла войти часть следующей дислокации. Начальную температуру задавали равной 0 К, но в процессе создания и движения дислокации расчетная ячейка нагревалась до температуры порядка 10 К.
Теоретически энергия дислокации W, приходящаяся на единицу ее длины l, определяется по формуле [7, 19]
| \(\frac{W}{l} = \frac{{\mu {b^2}}}{{4\pi K}}{\rm{ln}}\frac{R}{{{r_0}}},\) | (1) |
где μ – модуль сдвига; b – модуль вектора Бюргерса; R – радиус расчетной области; r0 – условный радиус; K – параметр, зависит от типа дислокации (K = 1 и K = 1 – ν для винтовой и краевой дислокации); ν – коэффициент Пуассона.
Энергия полной краевой дислокации для разных металлов может принимать значения 1 – 3 эВ/Å [7, 19, 20].
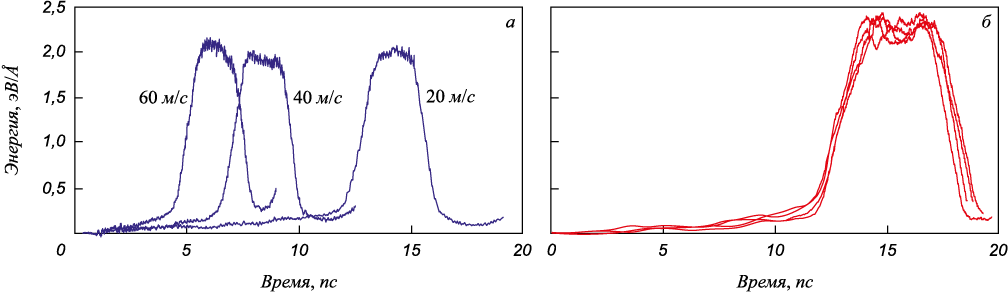
В первую очередь провели исследование влияния на энергию полных дислокаций (то есть всего комплекса из двух частичных плюс энергии дефекта упаковки между ними) ширины расчетной ячейки (размера вдоль оси X на рис. 1) и скорости сдвига Vτ . На рис. 2, а показано изменение удельной энергии расчетной области (эВ/Å) при прохождении полной краевой дислокации в γ-железе при разной скорости сдвига.
Рис. 2. Изменения энергии расчетной области при прохождении краевой дислокации в γ-железе |
Скорость сдвига Vτ , как можно видеть, практически не влияет на высоту пика энергии расчетной области, но до значений примерно 40 – 50 м/с. При скорости сдвига Vτ больше 40 – 50 м/с энергия слабо увеличивается из-за дополнительных напряжений и меньшего расстояния между соседними дислокациями. Скорость самих дислокаций при прохождении расчетной области при этом тоже увеличивается, что видно, например, по сравнительно более узкому пику для 60 м/с (рис. 2, а).
На рис. 2, б приведены изменения энергии расчетной области при прохождении краевой полной дислокации в стали Гадфильда в четырех расчетных ячейках с разным случайным распределением примесных атомов. Графики для разных образцов немного отличаются, но в целом картина схожая: энергия дислокации в стали чуть выше, чем в γ-железе, а скорость при тех же условиях существенно ниже, что можно легко оценить по ширине пиков на графиках. Скорость дислокации в стали ниже по вполне очевидным причинам: из-за торможения дислокации примесями, в основном, углерода, которые имеют положительную энергию связи как с дислокациями, так и с дефектами упаковки. В работах [21, 22], например, для энергии связи атомов углерода с дислокациями в ОЦК железе приводятся значения от 0,4 до 0,7 эВ в зависимости от типа и ориентации дислокации.
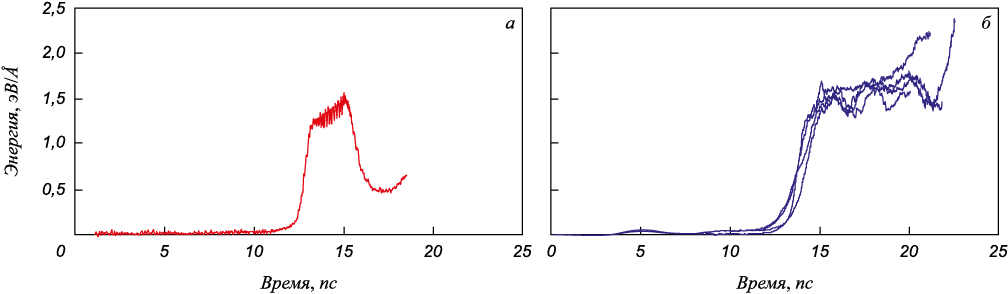
На рис. 3 приведены графики изменения энергии расчетной области для винтовой дислокации. Видно, что энергия винтовой дислокации заметно меньше, чем краевой. Как и для краевой, скорость винтовой дислокации в стали меньше, а энергия чуть больше. Кроме того, винтовая дислокация в стали могла остановиться в расчетной области или поменять плоскость скольжения с (111) на ( \(\bar 1\bar 11\)).
Рис. 3. Изменения энергии расчетной области при прохождении винтовой дислокации |
Энергия полной краевой дислокации в γ-железе и в стали Гадфильда составила в среднем 2,0 и 2,3 эВ/Å, винтовой – 1,3 и 1,5 эВ/Å соответственно.
Скорость движения дислокации определялась в модели с помощью анализа смещений атомов в двух реперных точках, расположенных вдоль оси движения дислокации Y. На рис. 4, а приведены полученные зависимости скорости краевой и винтовой дислокаций от скорости сдвига vτ . Средняя скорость дислокации с ростом скорости сдвига vτ , что очевидно, увеличивается. Но это, как известно, происходит до определенного предела, зависящего от скорости звука в металле [3, 6 – 8]. Скорость краевой дислокации (рис. 4, а) выше винтовой, что также является известным фактом и объясняется отличием скоростей распространения продольных и поперечных волн в материале [7, 8, 19].
Рис. 4. Зависимости скорости скольжения дислокаций от скорости сдвига |
Дислокации в стали Гадфильда при низких температурах двигались со скоростью, меньшей примерно в 1,5 раза, чем в γ-железе при тех же условиях. При слишком высоких скоростях сдвига (обычно уже выше 400 м/с) происходило дополнительное дефектообразование и даже разрушение кристаллической решетки. При винтовом типе сдвига разрушения начинались при еще меньших значениях: начиная примерно с 200 м/с.
С ростом температуры, согласно различным источникам [3, 6 ‒ 8], скорость дислокации снижается. На это влияют фононное рассеяние, зависимость от температуры модулей сдвига и т. д. Для учета факторов, тормозящих дислокацию, введен так называемый коэффициент сопротивления B [3, 6], скорость дислокации v записывается в виде [3]
| \(v = \frac{{\tau b}}{B},\) | (2) |
где τ – сдвиговое напряжение; b – модуль вектора Бюргерса.
Коэффициент сопротивления пропорционален температуре [6]:
| \(B = \frac{{3kzT}}{{10{b^2}{c_s}}},\) | (3) |
где k – постоянная Больцмана; z – количество атомов в элементарной ячейке; T – температура; cs – скорость поперечной волны.
Таким образом, согласно формуле (3), с ростом температуры скорость дислокации в металле уменьшается, что также подтверждается в модели для γ-железа (рис. 4, б). Однако для стали Гадфильда получен иной результат, где отчетливо проявилось влияние примесей. При низких температурах они тормозили дислокацию, их скорость примерно в 1,5 раза оказалась ниже, чем в γ-железе. С ростом температуры примерно до 500 К скорость дислокаций в стали, наоборот, возрастала, что, по всей видимости, объясняется интенсификацией диффузии примесных атомов углерода. При температуре примерно с 500 до 1100 К (рис. 4, б) скорость дислокации в стали почти совпадала с зависимостью для скорости дислокации в аустените, оставаясь чуть ниже. Но затем, при дальнейшем повышении температуры, снижалась более интенсивно, чем в чистом железе. Последнее связано, видимо, с влиянием примесей, вследствие дополнительного «фононного шума» от них и искажения кристаллической решетки.
Выводы
Методом молекулярной динамики проведено исследование скольжения краевой и винтовой дислокаций в стали Гадфильда и в γ-железе (аустените) в зависимости от температуры и скорости деформирования. Полная дислокация появлялась в настоящей модели сразу в виде расщепленной на пару частичных дислокаций Шокли, разделенных дефектом упаковки. Расстояние между частичными дислокациями составляло несколько нанометров. При увеличении скорости сдвига оно уменьшалось.
Согласно полученным данным, энергии краевой и винтовой дислокаций в стали оказались выше, чем в чистом аустените. Энергия полной краевой дислокации в γ-железе и в стали Гадфильда составила в среднем 2,0 и 2,3 эВ/Å, винтовой – 1,3 и 1,5 эВ/Å соответственно.
Получены зависимости скорости скольжения краевой и винтовой дислокаций от скорости сдвига и температуры. Скорость скольжения краевой дислокации во всех случаях была выше, чем винтовой, что объясняется отличием скорости распространения продольной и поперечной волн в материале. С ростом скорости сдвига скорость скольжения возрастала до определенного предела, зависящего от скорости распространения соответствующих упругих волн. При низких и нормальных температурах скорость скольжения дислокаций в стали Гадфильда оказалась существенно (примерно в полтора раза) ниже по сравнению с γ-железом. С ростом температуры скорость скольжения дислокаций в γ-железе уменьшается. Однако для стали Гадфильда эта зависимость оказалась немонотонной: сначала, по мере увеличения температуры примерно до 500 К скорость дислокаций возрастала, что связано, по всей видимости, с интенсификацией диффузии примесных атомов углерода, а затем, как и в железе, падала.
Список литературы
1. Chen C., Meng F., Ou P., Lan G., Li B., Chen H., Qiu Q., Song J. Effect of indium doping on motions of <a>-prismatic edge dislocations in wurtzite gallium nitride // Journal of Physics: Condensed Matter. 2019. Vol. 31. No. 31. Article 315701. https://doi.org/10.1088/1361-648X/ab1bf3
2. Olmsted D.L., Hector Jr. L.G., Curtin W.A., Clifton R.J. Atomistic simulations of dislocation mobility in Al, Ni and Al/Mg alloys // Modelling and Simulation in Materials Science and Engineering. 2005. Vol. 13. No. 3. P. 371–388. https://doi.org/10.1088/0965-0393/13/3/007
3. Zhao S., Osetsky Y.N., Zhang Y. Atomic-scale dynamics of edge dislocations in Ni and concentrated solid solution NiFe alloys // Journal of Alloys and Compounds. 2017. Vol. 701. P. 1003–1008. https://doi.org/10.1016/j.jallcom.2017.01.165
4. Rodney D., Ventelon L., Clouet E., Pizzagalli L., Willaime F. Ab initio modeling of dislocation core properties in metals and semiconductors // Acta Materialia. 2017. Vol. 124. P. 633–659. https://doi.org/10.1016/j.actamat.2016.09.049
5. Hunter A., Beyerlein I.J., Germann T.C., Koslowski M. Influence of the stacking fault energy surface on partial dislocations in fcc metals with a three-dimensional phase field dislocations dynamics model // Physical Review B. 2011. Vol. 84. Article 144108. https://doi.org/10.1103/PhysRevB.84.144108
6. Po G., Cui Y., Rivera D., Cereceda D., Swinburne T.D., Marian J., Ghoniem N. A phenomenological dislocation mobility law for bcc metals // Acta Materialia. 2016. Vol. 119. P. 123–135. https://doi.org/10.1016/j.actamat.2016.08.016
7. Фридель Ж. Дислокации. Москва: Мир, 1967. 660 с.
8. Хирт Дж., Лоте И. Теория дислокаций. Москва: Атомиздат, 1972. 600 с.
9. Zhang F.C., Lv B., Wang T.S., Zheng C.L., Zhang M., Luo H.H., Liu H., Xu A.Y. Explosion hardening of Hadfield steel crossing // Materials Science and Technology. 2010. Vol. 26. No. 2. P. 223‒229. https://doi.org/10.1179/174328408X363263
10. Chen C., Lv B., Ma H., Sun D., Zhang F. Wear behavior and the corresponding work hardening characteristics of Hadfield steel // Tribology International. 2018. Vol. 121. P. 389‒399. https://doi.org/10.1016/j.triboint.2018.01.044
11. Lau T.T., Forst C.J., Lin X., Gale J.D., Yip S., Van Vliet K.J. Many-body potential for point defect clusters in Fe-C alloys // Physical Review Letters. 2007. Vol. 98. Article 215501. https://doi.org/10.1103/PhysRevLett.98.215501
12. Oila A., Bull S.J. Atomistic simulation of Fe-C austenite // Computational Materials Science. 2009. Vol. 45. No. 2. P. 235‒239. https://doi.org/10.1016/j.commatsci.2008.09.013
13. Poletaev G.M., Rakitin R.Y. Molecular dynamics study of stress-strain curves for γ-Fe and Hadfield steel ideal crystals at shear along the <111> direction // Materials Physics and Mechanics. 2021. Vol. 47. No. 2. P. 237–244. https://doi.org/10.18149/MPM.4722021_6
14. Massardier V., Le Patezour E., Soler M., Merlin J. Mn-C interaction in Fe-C-Mn steels: study by thermoelectric power and internal friction // Metallurgical and Materials Transactions A. 2005. Vol. 36. P. 1745–1755. https://doi.org/10.1007/s11661-005-0039-x
15. Slane J.A., Wolverton C., Gibala R. Carbon–vacancy interactions in austenitic alloys // Materials Science and Engineering: A. 2004. Vol. 370. No. 1-2. P. 67–72. https://doi.org/10.1016/j.msea.2003.08.073
16. Poletaev G.M., Zorya I.V., Starostenkov M.D. Role of point defects in self-diffusion along low-angle twist boundaries in fcc metals: A molecular dynamics study // Journal of Micromechanics and Molecular Physics. 2018. Vol. 3. No. 1&2. Article 1850001. https://doi.org/10.1142/S2424913018500017
17. Poletaev G.M. Self-diffusion in liquid and solid alloys of the Ti–Al system: molecular-dynamics simulation // Journal of Experimental and Theoretical Physics. 2021. Vol. 133. No. 4. P. 455–460. https://doi.org/10.1134/S1063776121090041
18. Poletaev G.M., Starostenkov M.D. Dynamic collective displacements of atoms in metals and their role in the vacancy mechanism of diffusion // Physics of the Solid State. 2009. Vol. 51. No. 4. P. 727‒732. https://doi.org/10.1134/S106378340904012X
19. Cahn R.W., Haasen P. Physical Metallurgy. 4th ed. Amsterdam: North-Holland Physics Publishing, 1996. 2740 p.
20. Zhou X.W., Sills R.B., Ward D.K., Karnesky R.A. Atomistic calculations of dislocation core energy in aluminium // Physical Review B. 2017. Vol. 95. Article 054112. https://doi.org/10.1103/PhysRevB.95.054112
21. Veiga R.G.A., Goldenstein H., Perez M., Becquart C.S. Monte Carlo and molecular dynamics simulations of screw dislocation locking by Cottrell atmospheres in low carbon Fe-C alloys // Scripta Materialia. 2015. Vol. 108. P. 19–22. https://doi.org/10.1016/j.scriptamat.2015.06.012
22. Карькина Л.Е., Карькин И.Н., Яковлева И.Л., Зубкова Т.А. Моделирование диффузии углерода вблизи дислокации b/2[010](001) в цементите // Физика металлов и металловедение. 2013. Т. 114. № 2. С. 172–178. https://doi.org/10.7868/S0015323013020095
Об авторах
И. В. ЗоряРоссия
Ирина Васильевна Зоря, к.т.н., доцент, заведующий кафедрой теплогазоводоснабжения, водоотведения и вентиляции
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Г. М. Полетаев
Россия
Геннадий Михайлович Полетаев, д.ф.-м.н., профессор, заведующий кафедрой высшей математики и математического моделирования
Россия, 656038, Алтайский край, Барнаул, пр. Ленина, 46
Р. Ю. Ракитин
Россия
Роман Юрьевич Ракитин, к.ф.-м.н., доцент, директор колледжа
656038, Россия, Алтайский край, Барнаул, Комсомольский пр., 100
Рецензия
Для цитирования:
Зоря И.В., Полетаев Г.М., Ракитин Р.Ю. Энергия и скорость скольжения краевой и винтовой дислокаций в аустените и стали Гадфильда: молекулярно-динамическое моделирование. Известия высших учебных заведений. Черная Металлургия. 2022;65(12):861-868. https://doi.org/10.17073/0368-0797-2022-12-861-868
For citation:
Zorya I.V., Poletaev G.M., Rakitin R.Yu. Energy and velocity of sliding of edge and screw dislocations in austenite and Hadfield steel: Molecular dynamics simulation. Izvestiya. Ferrous Metallurgy. 2022;65(12):861-868. (In Russ.) https://doi.org/10.17073/0368-0797-2022-12-861-868