Scroll to:
Development of research on the physico-chemical properties of oxide and metal melts
https://doi.org/10.17073/0368-0797-2025-1-76-83
Abstract
The paper considers the historical development of scientific views on the structure of oxide and metal melts. The authors, using the research of the Ural Scientific School and their own works as examples, examine the evolution of approaches based on the polymer (ionic) theory of oxide melts and the cluster theory of liquid metals. The possibility of using a polymer model to determine the boundary of slag transition from a homogeneous state to a heterogeneous one and conditions for the formation of a homogeneous slag with maximum refining properties is shown. Al2O3 can exhibit both basic and acidic properties. It was found that with Al2O3 content of up to 16 % in oxide melts corresponding to the slags formed in ladle furnace unit, alumina exhibits basic properties, and when its content exceeds more than 16 %, it begins to exhibit acidic properties. Additional information on activities of the oxide melt components allows us to determine the parameters of the slag with the best properties for non-metallic inclusions absorption. Metal melt is characterized by a “critical” temperature at which the melt during heating transitions from hereditary cluster-type disequilibrium to a state of thermodynamic equilibrium, i.e., the melt “homogenizes”. Nonequilibrium melts temporarily retain elements of the structures of the initial phases. Overheating of the metal above the “critical” temperature during thermal-time treatment makes it possible to improve and stabilize the quality of products. Modification of the melt leads to a significant decrease in the amount of necessary overheating and acceleration of the homogeneous melt formation. Fundamental studies of the properties and structure of metal liquids showed the development of a new applied direction under the general name “thermal-time treatment”.
Keywords
For citations:
Sheshukov O.Yu., Nevidimov V.N., Nekrasov I.V., Metelkin A.A., Tsepelev V.S. Development of research on the physico-chemical properties of oxide and metal melts. Izvestiya. Ferrous Metallurgy. 2025;68(1):76-83. https://doi.org/10.17073/0368-0797-2025-1-76-83
Introduction
The ongoing advancement of steelmaking processes remains a pressing necessity. However, the development of new, more efficient technologies is only possible through a thorough analysis of experimental data and a deep understanding of their physico-chemical nature. Further progress in various scientific schools and research directions must be based on refining the theoretical foundations of metallurgical processes.
Metallurgical enterprises and research centers in the Ural region have traditionally played a key role in the development of the country’s industrial sectors. This study aims to analyze the historical development of research on the physico-chemical properties of oxide and metal melts.
Research materials and methods
The structure of oxide melts, which form the basis of steelmaking slags, can be studied both through experimental methods and by evaluating the practical applicability of different theoretical models. When considering existing models of slag melt structure, we believe particular attention should be given to the polymer model.
The idea that oxide melts exhibit polymeric behavior was first proposed by Professor O.A. Esin in 1946 [1]. Based on the ionic nature of these melts, Esin suggested that oxide melts contain silicate-oxygen anions of varying complexity, which are in chemical equilibrium with each other and with “free” oxygen ions.
In general, this equilibrium can be expressed as
| \[{\rm{S}}{{\rm{i}}_i}{\rm{O}}_{3i + 1}^{2(i + 1) - } + {\rm{SiO}}_4^{4 - } = {\rm{S}}{{\rm{i}}_{i + 1}}{\rm{O}}_{3i + 4}^{2(i + 2) - } + {{\rm{O}}^{2 - }}.\] | (1) |
Over time, this assumption became the foundation for various polymer models of silicate melts. Some models (non-structural) do not explicitly account for the structure of anions, whereas others (structural) focus primarily on the arrangement of complex anions.
Pioneering studies in this field were conducted by G.V Toop and C.S. Samis in 1962 [2], as well as by C.R. Masson in 1965 [3]. Within the framework of the non-structural model, they were the first to provide a quantitative assessment of the distribution of “free”, terminal, and bridging oxygen atoms in binary silicate melts and formulated the equilibrium constant for the polymerization reaction (1) as follows:
| \[{K_{\rm{P}}} = \frac{{{n_{{{\rm{O}}^{2 - }}}}{n_{{{\rm{O}}^0}}}}}{{n_{{{\rm{O}}^ - }}^2}},\] | (2) |
where \({n_{{{\rm{O}}^{2 - }}}}\), \({n_{{{\rm{O}}^ - }}}\) and \({n_{{{\rm{O}}^0}}}\) represent the number of moles of О2‒, О‒ and О0, per mole of binary silicate melt.
In studies [3 – 6], a structural model was proposed. This model assumes that, in addition to Men+ cations, “free” О2‒ oxygen ions, and monomers \({\rm{SiO}}_4^{4 - }\) the binary silicate melt contains only chain-like anions of type \({\rm{S}}{{\rm{i}}_i}{\rm{O}}_{3i + 1}^{2(i + 1) - }\), which may be either linear or branched. The formation of ring and network structures is excluded, meaning that the model applies to binary silicate melt compositions in the MeO ‒ SiO2 system within the range 0 ≤ \({x_{{\rm{Si}}{{\rm{O}}_2}}}\) ≤ 0.5.
The approach of C.R. Masson, I.B. Smith, and S.G. Whiteway was examined across the entire composition range in studies [7; 8] and compared with previous research [4 – 6]. The developed mathematical framework demonstrated strong convergence between calculated and experimental data throughout the investigated composition range.
A considerable number of studies in the literature have focused on extending polymer models of binary silicate melts to multicomponent systems. For example, in [9], the model equations were generalized for ternary systems Me′O ‒ Me″O ‒ SiO2 , with the assumption that Me′ n+ and Me″ n+ cations are randomly distributed and that the degree of melt polymerization is a function of the polymerization constants in binary silicate melts.
Alongside the development of theoretical models describing the structure of silicate melts, experimental studies have been conducted using modern physico-chemical methods.
The application of the analytical method of trimethylsilylation in combination with gas chromatography [10] and paper chromatography [11], as well as ultrasonic investigations [12], confirms the presence of both complex silicate-oxygen structures (SiO2)i , which represent the ultimate form of complex anions \({\rm{S}}{{\rm{i}}_i}{\rm{O}}_{3i + 1 - c}^{2(i + 1 - c) - }\) (with a self-closing number с = 1 for planar rings), and only the simplest silicate anions: monomers \({\rm{SiO}}_4^{4 - }\), short linear chains \({\rm{S}}{{\rm{i}}_{\rm{2}}}{\rm{O}}_7^{6 - }\) and \({\rm{S}}{{\rm{i}}_{\rm{3}}}{\rm{O}}_{10}^{8 - }\), as well as planar rings.
It is important to note that no isomeric forms of anions, such as branched chains, have been identified in crystalline, glassy, or liquid silicates.
The findings from these studies contributed to the development of a refined version of the polymer model that accounts for the variable functionality of the monomer [13]. According to this model, the monomer \({\rm{SiO}}_4^{4 - }\) is bifunctional (f = 2) in chain-like anions, meaning that only two of the four terminal oxygen atoms in the silicate-oxygen tetrahedron participate in reactions. In cyclic ions, however, the monomer \({\rm{SiO}}_4^{4 - }\) is tetrafunctional (f = 4). The polymer model suggests that the average functionality of the monomer varies from two (in a fully depolymerized melt) to four (in pure SiO2 ), increasing progressively as the degree of polymerization rises. Based on this model, equations were derived to quantitatively describe the structural units and component activities in binary silicate melts. These equations were further applied to develop a theoretical framework for calculating the activity of multicomponent oxide melts containing different complex-forming elements.
In steelmaking, the theory of oxide melts is widely used to evaluate the refining properties of slags, the formation of slag crust, and the generation of oxide-based non-metallic inclusions (NMI).
One example of this application is the use of the polymer model to analyze the characteristics of slag melts used in ladle treatment of steel and the formation of oxide-based NMI. To understand how the chemical composition of slag melts (wt. %) influences the thermodynamic activity of components, the melt with a fixed content of magnesium and silicon oxides (11.11 % MgO; 16.67 % SiO2 ) was studied, where a portion of lime was replaced with an alumina-based flux. The content of CaO varied from 33.33 to 55.56 %, while Al2O3 ranged from 16.76 to 38.89 %, meaning that CaO was progressively substituted with Al2O3 .
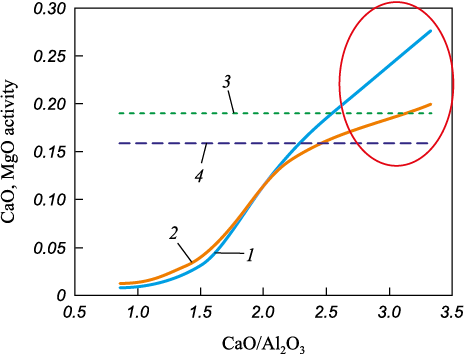
Using the polymer model, it is possible to calculate the activity of CaO and MgO in the melt, as well as their saturation activity (saturation limits) depending on the CaO/Al2O3 ratio (Fig. 1).
Fig. 1. Activities of CaO and MgO oxides in the melt for slag |
These data on the activity of CaO and MgO oxides are particularly important for analyzing the refining properties of slags [14] and understanding the mechanisms behind the formation of calcium- and magnesium-containing aluminate NMI in steel [15].
A significant increase in CaO concentration causes basic oxides to transition into the solid phase. Thus, the polymer model helps determine the boundary at which slags shift from a homogeneous to a heterogeneous state, ensuring the formation of exclusively homogeneous slags (Fig. 1) with maximum desulfurization capacity and an enhanced ability to absorb NMI.
While the behavior of CaO, MgO, and SiO2 oxides is well understood, as they act as basic and acidic components, Al2O3 is an amphoteric compound that can exhibit both basic and acidic properties. It has been established that in oxide melts – corresponding to slags formed in ladle furnace units and secondary steel refining systems – alumina exhibits basic properties when its content does not exceed 16 %. However, once its concentration surpasses 16 %, it begins to display acidic characteristics [16].
Information on activity values allows for the determination of the parameters of slag melts with the highest capacity for NMI absorption. In particular, the activity values of Al2O3 and SiO2 play a key role in evaluating the slag’s ability to absorb and dissolve aluminate and silicate NMIs. Based on the model describing the transfer of NMIs into slag [17], it can be concluded that the dissolution of NMIs in slag is a critical stage in the steel refining process. To analyze this process, the approach, that traditionally employed to describe the dissolution of refractory particles in slag, is applicable [18]:
| \[Q = \frac{D}{\Delta }S({C_{sat}} - C),\] | (3) |
where Q is the dissolution rate of the solid phase (refractory material or NMI) in the slag, D is the diffusion coefficient of the solid-phase material in the slag, S is the contact area between the solid phase and the slag, Δ is the thickness of the diffusion layer, Сsat is the saturation concentration of the slag with the solid-phase material, С is the current concentration of the solid-phase material in the slag.
If the parameters D and Δ in equation (3) are expressed in terms of their known dependencies on slag viscosity, it becomes possible to determine the dissolution rate of non-metallic inclusions
| \[Q \sim \frac{{{C_{{\rm{sat}}}} - C}}{{{{\left( {\frac{\eta }{\rho }} \right)}^{\frac{5}{6}}}}}.\] | (4) |
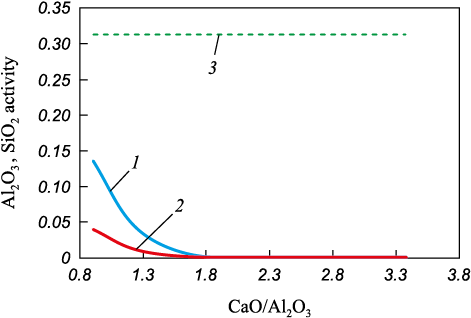
Al2O3 and SiO2 oxides are the largest and least mobile components of the slag, forming the primary physical mass of silicate and/or aluminate NMI. As a result, these components are expected to control the flow behavior, diffusion mechanism, and dissolution processes of the slag components. The slag’s saturation with NMI material should be assessed based on its proximity to saturation with SiO2 and Al2O3 . The corresponding calculated data are presented in Fig. 2.
Fig. 2. Activities of Al2O3 and SiO2 oxides in the melt for slag formation |
A comparison of the calculated data suggests that the method of oxide melt formation plays a decisive role in determining its characteristics. This conclusion helps explain the discrepancies observed in practical recommendations regarding the optimal slag composition and the type of deoxidizers used to achieve the desired steel purity [18; 19].
Possible applications of experimental data in research on the ionic theory of slags include determining optimal slag compositions with optimal parameters, such as maximum sulfide capacity and enhanced ability to absorb non-metallic inclusions, as well as identifying the optimal slag compositions at various stages of the steelmaking process.
One of the key research areas developed by the Ural Scientific School is the study of the characteristics of metal melts. This research has been actively pursued since the 1950s at the Ural Polytechnic Institute named after S.M. Kirov, within the Department of Physics under the leadership of Pavel Vladimirovich Geld [20; 21].
According to modern concepts, the liquid state of matter occupies an intermediate position between the crystalline and gaseous states on the temperature scale. From a metallurgical perspective, this task is somewhat simplified, as the liquid state of metals is typically considered within the temperature range from the melting point Tm to approximately 1.25Tm . This range is close to the melting and crystallization points and is often referred to as the melt. Both the crystalline and liquid states are condensed phases in which interatomic attractive forces play a dominant role, unlike in the gaseous phase. By definition, the gas phase is characterized by chaos, the condensed phase – by order, in crystals it is distant, and in the melt it is near.
Experimental data were confirmed through studies of the fundamental properties of metal melts, such as density and electrical resistivity, using differential thermal analysis and X-ray analysis [21; 22]. The results indicate that the decrease in density upon melting of normal and transition metals ranges from 1 to 3 %, primarily due to the formation of “voids” and cavities within the structure. X-ray studies conducted by E.Z. Spektor and A.V. Romanova, later supported by other researchers, demonstrated that during melting, the most probable nearest interatomic distances do not increase – in fact, they may even decrease (including in iron). This suggests that attractive forces cause the atoms of the melt to cluster into aggregates or sibotaxies, with free volume distributed between clusters, containing individual atoms of the heated melt.
To refine this concept further, clusters can be understood as structures formed by the specific attractive forces characteristic of a given type of atom. As a result, each cluster retains a distinctive structure similar to that of its precursor, the crystal. Meanwhile, interatomic interactions and the intensity of thermal motion increase by a factor of KΔТ, where K = 1.38·10‒23 J/K and ΔT is the absolute temperature increment. It is evident that quasi-crystalline order within a cluster becomes blurred due to thermal motion, particularly at boundaries where cavities and free volume are present. Consequently, clusters lack sharply defined boundaries, gradually transitioning into a disordered zone, the proportion of which increases with temperature and becomes significant at temperatures above 1.5Тm .
As a result, the transition from a pure metal to a multicomponent melt further complicates its structure. Various interactions within the cluster – metallic, covalent, resonant, or other specific types of bonding – determine its internal arrangement and stability over time. Indirect insights into these and other characteristics can be obtained through physico-chemical analysis methods, particularly by studying the temperature and concentration dependencies of the physical properties of melts.
One of the most significant findings is that a melt, even if it matches the specified chemical composition, is not always ready for casting. Over time, dangerous defects may appear in finished products made from such a melt, including rails, pipes, and machine components, ultimately leading to structural failure. This thermodynamic system is far from equilibrium, and the influence of inherited phase components from the charge material is quite pronounced. These components transfer their numerous local atomic arrangements, as well as chemical and physical microinhomogeneities, to the melt. Convective mixing and bubbling caused by rising carbon monoxide or argon gas bubbles can only partially equalize these inhomogeneities on a microscopic level. The most effective way to eliminate inherited non-equilibrium atomic groupings is to heat the melt to its critical temperature (tc ), at which the average thermal energy of a particle becomes comparable to the activation energy required for it to break away from its parent associate.
According to the obtained data, the term “critical temperature” (tc ) is used to designate specific points on the temperature scale at which a system transitions into a single-phase equilibrium state. These include the critical temperature of equilibrium coexistence between liquid and vapor, the critical temperature of mutual unlimited solubility in liquid mixtures, and the critical temperature associated with the loss of superconductivity or superfluidity.
It is believed that tc represents the temperature at which a melt, upon heating, transitions from a hereditary cluster-type nonequilibrium state into a thermodynamically equilibrium state. However, if a melt transitions from a multiphase state (such as a suspension or emulsion) to a single-phase state, the term “melt homogenization” is more appropriate than tc .
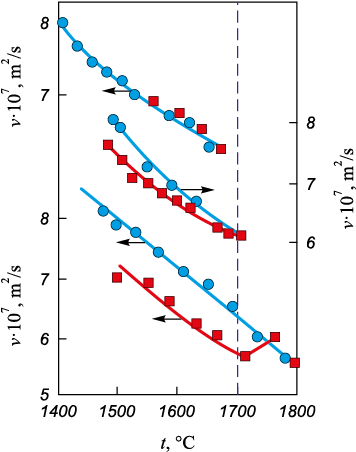
A reliable and convenient instrumental method for determining tc is based on melt viscometry. This approach involves detecting discrepancies in viscosity values between heating and cooling cycles (Fig. 3). Such discrepancies appear only at a certain overheating level above the liquidus temperature [21]. The position of the reverse viscosity curve (obtained during cooling) depends on the relationship between the maximum heating temperature of the studied metal sample and the temperature at which polytherm branching begins. If the maximum heating temperature does not reach the anomaly temperature, hysteresis (branching) does not occur; it only manifests when tc is exceeded.
Fig. 3. Viscosity of Fe ‒ 30 % Ni melt depending on the maximum heating temperature |
Hysteresis in melt properties reflects hysteresis in its structure. This is why comprehensive studies of melt properties provide insights into its structure, and the obtained results remain independent of the sample volume, as the observed processes occur at a kinetic scale on the microlevel. The value of tc depends on the steel grade, the phase composition of the charge, and the melting conditions. Heating the melt to tc is a method of bringing the system into equilibrium. However, excessive overheating beyond tc can be technologically more detrimental than underheating, as it significantly increases gas saturation in the metal and intensifies interactions with the refractory lining, among other effects.
Thus, nonequilibrium melts temporarily retain structural elements of their initial phases. In contrast, the structure and properties of equilibrium, and therefore maximally homogeneous, systems are determined not by their history but by their chemical composition and temperature. Casting an equilibrium melt ensures a stable crystallization process from one heat to another, resulting in optimal ingot and casting structures and consistently high product quality [21].
Fundamental studies on the properties and structure of liquid metals have led to the emergence of a new applied field – technologies for transitioning multicomponent metal melts into an equilibrium state to improve and stabilize product quality. This approach has become known as “thermal-time treatment” [21].
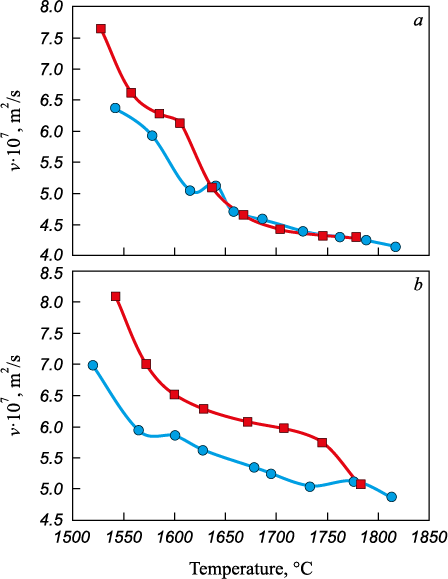
Further research in this field has demonstrated the possibility of improving classical thermal-time treatment. It has been established that the required overheating can be significantly reduced, and the formation of a microhomogeneous melt can be accelerated through modification. For example, introducing an optimal amount of a calcium-containing modifier into steel has been shown to lower tc from 1780 ‒ 1800 to 1630 ‒ 1640 °С, making it technologically achievable (Fig. 4).
Fig. 4. Polytherms of kinematic viscosity of the melt of 20tr steel: |
These findings have significant industrial implications, enabling the development of technological solutions for controlling the properties of steel in both its liquid and solid states.
Conclusion
Building on the work of the Ural Scientific School and the authors’ own research, an attempt has been made to analyze the historical development of scientific concepts regarding the structure of oxides and molten iron. The study explores the emergence of methods based on the polymer (ionic) theory of oxide dissolution and the theory of liquid-metal clusters. The potential applications of the polymer model for determining the transition boundary of slag from a homogeneous to a heterogeneous state and the conditions for forming a homogeneous slag with high refining properties are also presented. The research confirms that under ideal conditions, Al2O3 oxide can exhibit both basic and acidic properties. When its concentration in an oxide melt reaches 16 %, alumina acts as a basic component. However, when its content exceeds 16 %, it begins to exhibit acidic properties.
References
1. Esin O.A. The Electrolytic Nature of Liquid Slags. Sverdlovsk: Ural Industrial Institute; 1946:41. (In Russ.).
2. Toop G.V., Samis C.S. Activities of ions in silicate melts. Transactions of Metallurgical Society AIME. 1962;224(5): 878–887.
3. Masson C.R. An approach to the problem of ionic distribution in liquid silicates. Proceedings of the Royal Society A. 1965;287(1409):201–221. https://doi.org/10.1098/rspa.1965.0176
4. Whiteway S.G., Smith I.B., Masson C.R. Theory of molecular size distribution in multichain polymers. Canadian Journal of Chemistry. 1970;48(1):33–45. https://doi.org/10.1139/v70-006
5. Masson C.R., Smith I.B., Whiteway S.G. Molecular size distribution in multichain polymers: application of polymer theory to silicate melts. Canadian Journal of Chemistry. 1970;48(1):201–202. http://doi.org/10.1139/v70-033
6. Masson C.R., Smith I.B., Whiteway S.G. Activities and ionic distribution in liquid silicates: application of polymer theory. Canadian Journal of Chemistry. 1970;48(9):1456–1464. https://doi.org/10.1139/v70-238
7. Esin O.A. Application of polymer theory to molten slags. In: Physico-Chemical Studies of Metallurgical Processes: Interuniversity Proceedings. Sverdlovsk: UPI; 1973;1:5–17. (In Russ.).
8. Esin O.A. On application of a polymer model, taking into account isomeric forms, to molten silicates. In: Physico-Chemical Studies of Metallurgical Processes: Interuniversity Proceedings. Sverdlovsk: UPI; 1976;4:17–27. (In Russ.).
9. Yokokawa T., Niwa K. Free energy and basicity of molten silicate solution. Transactions of the Japan Institute of Metals. 1969;10(2):81–84. https://doi.org/10.2320/matertrans1960.10.81
10. Smart R.M., Glasser F.P. Silicate anion constitution of lead silicate glasses and crystals. Physics and Chemistry of Glasses. 1978;19(5):95–102.
11. Wieker W., Hoebbel D., Götz J. Die Anionenverteilung in Silikatgläsern und ihre Bedeutung für die Glasbildung. Wissenschaftliche Zeitschrift Friedrich–Schiller-Univ. 1979;28(2-3):277–285. (In Germ.)
12. Baidov V.V. Ultraacoustic studies and microstructure of silicate melts. In: Properties and Structure of Slag Melts. Moscow: Nauka; 1970:23–38. (In Russ.).
13. Novikov V.K., Nevidimov V.N. Polymeric Nature of Molten Slags. Yekaterinburg: USTU–UPI; 2006:62. (In Russ.).
14. Sheshukov O.Yu., Nekrasov I.V., Metelkin A.A., Lozovaya E.Yu., Shevchenko O.I., Savel’ev M.V. Modern Steel: Theory and Technology. Yekaterinburg: UrFU; 2020:400. (In Russ.).
15. Khoroshilov A.D. Analysis and development of technology for ladle processing of ultra-low carbon steels in order to improve the surface quality of rolled steel. Extended abstract of Cand. Sci. Diss. Moscow; 2022:19. (In Russ.).
16. Sheshukov O.Yu., Mikheenkov M.A., Nekrasov I.V., Egiazar’yan D.K., Metelkin A.A., Shevchenko O.I. Issues of Utilization of Refining Slags of Steelmaking Production. Nizhny Tagil: NTI (Branch) UrFU; 2017:208. (In Russ.).
17. Deryabin V.A., Deryabin A.A. Thermodynamic features of transition of solid nonmetallic inclusions from metal to slag. Izvestiya. Ferrous Metallurgy. 1990;33(10):8–9. (In Russ.).
18. Nekrasov I.V., Sheshukov O.Yu., Nevidimov V.N., etc. Assessment of slag aggressiveness to non-metallic inclusions. In: Structure and Properties of Metal and Slag Melts. Proceedings of the XIII Russ. Conf. Yekaterinburg: UB RAS; 2011:16–19. (In Russ.).
19. Sheshukov O.Yu., Nekrasov I.V., Mikheenkov M.A., Egiazar’yan D.K., Ermakova V.P., Smirnova V.G., Chashchin A.A., Kalimullin E.V. Slag mode of a ladle furnace unit and modification efficiency. Ferrous Metallurgy. Bulletin of Scientific, Technical and Economic Information. 2015;(9(1389)):38–43. (In Russ.).
20. Sheshukov O.Yu., Nekrasov I.V., Bonar’ S.N., Egiazar’yan D.K., Tsymbalist M.M., Sivtsov A.V. Sulfide capacity of alumina slags of ladle-furnace steel treatment and activity of oxygen anions. Ferrous Metallurgy. Bulletin of Scientific, Technical and Economic Information. 2017;(2(1406)): 30–33. (In Russ.).
21. Gel’d P.V., Baum B.A., Petrushevskii M.S. Ferroalloy Melts as Liquid Alloys of Transition Metals with Silicon and Carbon. Moscow: Metallurgiya; 1973:288. (In Russ.).
22. Baum B.A., Khasin G.A., Tyagunov G.V., etc. Liquid Steel. Moscow: Metallurgiya; 1984:208. (In Russ.).
23. Sheshukov O.Yu., Nekrasov I.V., Ermakova V.P., Marshuk L.A., Egiazar'yan D.K., Lapin M.V., Shamanov A.N., Kovrizhnykh A.V., Akchibash A.O., Shvedov D.P., Tokarev A.S. Method of ladle-furnace treatment of steel with calcium. Pat. RF 2535428 C1. Byulleten' izobretenii. 2014;12. (In Russ.).
24. Nekrasov I.V., Sheshukov O.Yu., Tsepelev V.S. Structure of iron melts and promising technologies. In: Proceedings of Int. Sci. Conf. “Physico-Chemical Foundations of Metallurgical Processes” named after Academician A.M. Samarin. Vyksa: Vyksunskii metallurgicheskii zavod; 2022:131–135. (In Russ.).
25. Sheshukov O.Yu., Nekrasov I.V., Konashkov V.V., Egiazar’yan D.K. Structure-sensitive properties of steel melt: Efficiency evaluation of steel treatment with modifiers and fining clinkers. Elektrometallurgiya. 2019;(2):2–12. (In Russ.).
About the Authors
O. Yu. SheshukovRussian Federation
Oleg Yu. Sheshukov, Dr. Sci. (Eng.), Prof., Director of the Institute of New Materials and Technologies, Ural Federal University named after the first President of Russia B.N. Yeltsin, Chief Researcher, Institute of Metallurgy, Ural Branch of the Russian Academy of Sciences
19 Mira Str., Yekaterinburg 620002, Russian Federation
101 Amundsena Str., Yekaterinburg 620016, Russian Federation
V. N. Nevidimov
Russian Federation
Vladimir N. Nevidimov, Cand. Sci. (Eng.), Assist. Prof. of the Chair of Theory of Metallurgical Processes of the Institute of New Materials and Technologies
19 Mira Str., Yekaterinburg 620002, Russian Federation
I. V. Nekrasov
Russian Federation
Il’ya V. Nekrasov, Cand. Sci. (Eng.), Assist. Prof. of the Chair of Metallurgy of Iron and Alloys of the Institute of New Materials and Technologies
19 Mira Str., Yekaterinburg 620002, Russian Federation
A. A. Metelkin
Russian Federation
Anatolii A. Metelkin, Dr. Sci. (Eng.), Assist. Prof. of the Chair of Metallurgy of Iron and Alloys of the Institute of New Materials and Technologies
19 Mira Str., Yekaterinburg 620002, Russian Federation
V. S. Tsepelev
Russian Federation
Vladimir S. Tsepelev, Dr. Sci. (Eng.), Assist. Prof., Prof. of the Chair of Life Safety in the Technosphere, Director of the Research Center for Physics of Metallic Liquids
19 Mira Str., Yekaterinburg 620002, Russian Federation
Review
For citations:
Sheshukov O.Yu., Nevidimov V.N., Nekrasov I.V., Metelkin A.A., Tsepelev V.S. Development of research on the physico-chemical properties of oxide and metal melts. Izvestiya. Ferrous Metallurgy. 2025;68(1):76-83. https://doi.org/10.17073/0368-0797-2025-1-76-83