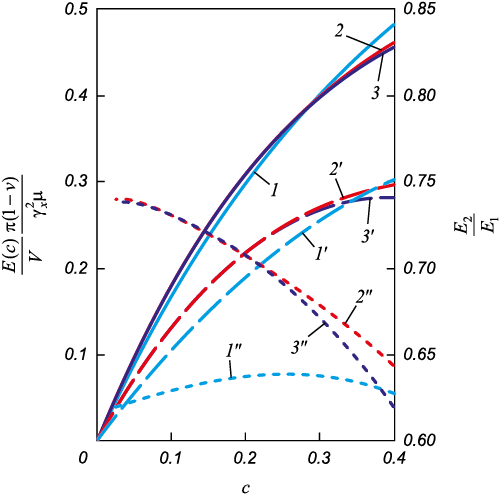Scroll to:
Influence of inhomogeneities in chemical composition and porosity of sintered steel on development of martensitic transformation
https://doi.org/10.17073/0368-0797-2024-4-417-423
Abstract
The article is devoted to the study of martensitic transformation in porous sintered steels. When analyzing the process of development of martensitic transformation in porous sintered steel, the influence of two factors was assessed: depletion of carbon in the near-surface layers of pores and a change in the energy balance due to relaxation of transformation stresses on free surfaces of the pores. The martensitic transformation was studied in porous steel with a carbon content of 1.56 wt. % obtained after pressing and sintering of a mixture of PZhRV iron powders and GK-3 graphite in hydrogen atmosphere at 1200 °C. Gas carburizing at 1100 °C and homogenization helped to achieve the specified carbon content. The samples were quenched in a sodium chloride solution at a temperature of 27 °C. Pre-cooling was used from temperatures Ast to 800 °C at a rate of 62 °C/s. X-ray microanalysis of carbon distribution was carried out using the installation CAMECA Microsonde M.S. 46 with a probe diameter of two microns. The martensite plates predominantly formed on the pores’ surfaces and their cross section had shape close to rhomboidal. The data obtained on the morphology of α′-phase crystals growing from pores and the study by X-ray spectral microanalysis of carbon distribution along the largest martensite plates convince us of the absence of any significant changes in carbon content and, as a consequence, their influence on development of martensitic transformation in the area of pores is not the leader. For sintered porous steels, an irremovable factor in the increase in temperature is the presence of porosity, in contrast to a removable factor – inhomogeneity of the chemical composition, which is caused by incompleteness of the alloy homogenization processes, both during sintering and during the austenitization process that precedes quenching.
For citations:
Pustovoit V.N., Dolgachev Yu.V., Egorov M.S., Vernigorov Yu.M. Influence of inhomogeneities in chemical composition and porosity of sintered steel on development of martensitic transformation. Izvestiya. Ferrous Metallurgy. 2024;67(4):417-423. https://doi.org/10.17073/0368-0797-2024-4-417-423
Introduction
The characteristics of martensitic transformation in porous sintered steels have been studied in considerable detail [1 – 3]. For sintered steels, an increase in the Ms point (martensite start temperature) is characteristic as porosity (the ratio of pore volume to the total volume of the product) increases. This phenomenon is generally explained by the reduction in resistance to plastic deformation in the γ-phase, which is characteristic of martensitic transformation [1; 4; 5]. However, the nucleation of martensite occurs in regions with significantly smaller diameters than those of the pores and the distances between them, so considering the properties of steels with normal density allows for a more precise understanding of nucleation processes. Additionally, the influence of the free surface on the nucleation of martensite needs to be studied. Thus, elastic interactions between martensite crystals and the free surfaces of pores can play a decisive role in the development of the martensitic reaction in sintered steels. Another potential reason for the increase in the Ms point could be segregation factors, which often occur in sintered steel due to segregation processes and incomplete solubility between components [1; 6 ‒ 8]. The factor of decarburization, leading to a shift in the Ms point due to the formation of carbides along pore boundaries (near the surface) during quenching, cannot be excluded. A similar effect has been observed during the precipitation of cementite and other carbides at grain boundaries. In studies [9; 10], carbide precipitation was associated with grain boundary segregation processes of sulfur, which induces carbon mobility. In porous sintered steel, concentrations of S and P are ≤ 0.05 % and О2 is ≤ 0.25 %, so segregation processes at various types of boundaries are also possible. The studies [11; 12] considered martensitic transformation that can be initiated by carbide precipitates during the aging of high-alloy austenitic steels. These processes also need to be examined for porous sintered steels.
In this study, we examined the martensitic transformation in sintered steels, considering the potential for carbon depletion in areas near the surface of the porous material and alterations in the energy balance resulting from relaxation processes occurring at the pores.
Research methodology
The potential influence of chemical composition inhomogeneities near the pores on the γ → α transformation was evaluated in experiments with samples obtained by sintering PZhRV iron and GK-3 graphite powders. The pressing and sintering were conducted in a hydrogen atmosphere at a temperature of 1200 °C for half an hour, resulting in a carbon concentration of 1.25 %, which was subsequently increased to 1.56 % during the carburizing process at 1100 °C and homogenization annealing.
Quenching was performed in an aqueous NaCl solution at a temperature of 27 °C. Pre-cooling was also applied before quenching, reducing the temperature from above the SE line to 800 °С at a rate of approximately 62 °C/s.
The carbon distribution was analyzed using X-ray microanalysis with a CAMECA Microsonde M.S. 46 system with a probe radius of 2 µm.
Results and discussion
Microstructural analysis revealed that martensite crystals predominantly formed at the surfaces of pores, with the crystals exhibiting a near-rhomboidal shape (Fig. 1, a, b). Twinned crystals ranging in size from 40 to 60 µm were also observed (Fig. 1, c).
Fig. 1. Microstructure of sintered Fe – 1.56 % C steel after quenching: |
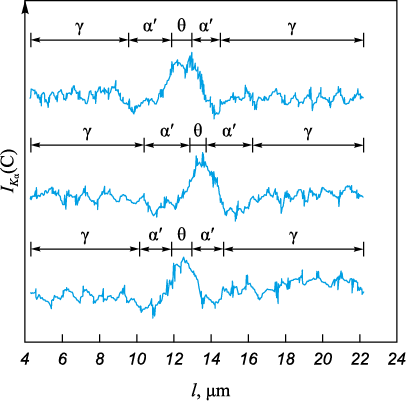
Cooling down induced the precipitation of Fe3C at grain boundaries, as well as within the γ-matrix. Consequently, the subsequent quenching led to the formation of martensite in carbon-depleted austenitic regions adjacent to cementite plates, characterized by a mixed crystal morphology with a predominant lath structure (Fig. 2, a, b). In microvolumes of austenite free from cementite precipitates, twinned martensite was observed (Fig. 2, b). Near the carbide formations, regions of low-carbon α′-phase with various morphological types, approximately 3 µm in size, were found (Fig. 2, b). Decarburization near the Fe3C plates was detected, as confirmed by X-ray microanalysis (Fig. 3). The thicknesses of the decarburized layer near Fe3C, determined by both X-ray microanalysis and microstructural analysis, were consistent.
Fig. 2. Structure of porous Fe – 1.57 % C steel with carbides released during cooling-down:
Fig. 3. Results of microanalysis (intensity of Kα-radiation C) |
In cases where the γ → α′ transition at the pore edge is initiated by decarburization, this should be distinctly observable in microstructural analysis. However, the morphological analysis of martensite crystals formed from the pore, along with the results from X-ray microanalysis of carbon concentration near the largest α′-phase crystals (Fig. 1, c), did not reveal significant differences in carbon content. Consequently, their influence on the γ → α′ transition process in the pore region appears to be negligible.
The influence of porosity on the transformation during quenching was theoretically analyzed, taking into account the potential for stress relaxation at the free surface of the pores, which occurs during transformation. It was assumed that, in the case of heterogeneous nucleation, part of the free energy associated with interactions between martensite and defects remains unchanged in the pore region and between the pores. It was considered that nucleation from the pore edge would occur if the other components of free energy necessary for homogeneous nucleation at the pores and between them were identical. Additionally, it was assumed that the form of the energy function for both cases remains constant. Thus, the free energy values were equated for homogeneous nucleation at the pores and between them when the nucleus reached the critical radius r\(^*\).
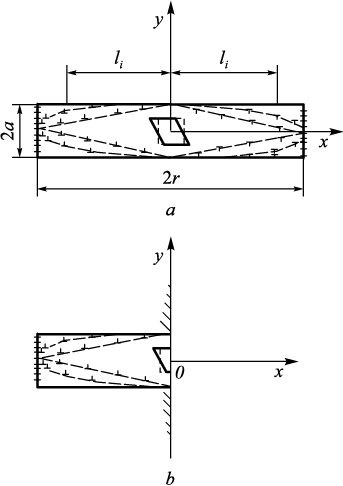
Fig. 4. Representation of the cross-section of martensite nuclei ofellipsoidal, |
The martensite crystal was modeled as a flat nucleus with elliptical, rectangular, and rhomboidal shapes (Fig. 4). Shear deformation was modeled using continuously distributed dislocations [13 ‒ 15]. The elastic shear energy during nucleation can be determined as follows [16]:
| \[{E_1} = \frac{1}{2}\sum\nolimits_i {\int_{{S_i}} {{b_i}\overline \sigma _{x,y}^0\left( {x,{Y_i}} \right)d{S_i}} } ,\] | (1) |
where bi is the Burgers vector of the i-th dislocation loop; \(\overline \sigma _{x,y}^0\) is the shear stress induced by the dislocation ensemble; Yi is the ordinate of the i-th loop plane; Si is the cross-sectional area of the plate in the i-th loop plane.
Then,
| \[\overline \sigma _{x,y}^0 = \sum {\overline \sigma _{x,y}^j} ;\] | (2) |
| \[\begin{array}{c}\overline \sigma _{x,y}^j(x,y) = \frac{{\mu {b_i}}}{{2\pi (1 - v)}} \times \\ \times \left[ {\frac{{\left( {x + {l_j}} \right)\left[ {{{\left( {x + {l_j}} \right)}^2} - {{\left( {y - {Y_j}} \right)}^2}} \right]}}{{{{\left[ {{{\left( {x + {l_j}} \right)}^2} + {{\left( {y - {Y_j}} \right)}^2}} \right]}^2}}} - \frac{{\left( {x - {l_j}} \right)\left[ {{{\left( {x - {l_j}} \right)}^2} - {{\left( {y - {Y_j}} \right)}^2}} \right]}}{{{{\left[ {{{\left( {x - {l_j}} \right)}^2} + {{\left( {y - {Y_j}} \right)}^2}} \right]}^2}}}} \right],\end{array}\] | (3) |
where μ is the shear modulus; v is Poisson’s ratio; lj is the absolute value of the j-th loop abscissa; bi = |Yj – Yj + 1| γx ; γx is the macroscopic shear along the x-axis (assuming \(\gamma _y^2 \ll \gamma _x^2\), dilation is not considered).
In the case of growth from a pore (Fig. 4, b) of a nucleus with the same cross-sectional area, the elastic energy is determined by similar dependencies:
| \[{E_2} = \frac{1}{2}\sum\nolimits_i {\int_{{S_i}} {{b_i}{{\overline \sigma }_{x,y}}\left( {x,{Y_i}} \right)d{S_i}} } ;\] | (4) |
| \[{\overline \sigma _{x,y}} = \sum {\overline \sigma _{x,y}^j + \overline \sigma _{x,y}^ + } .\] | (5) |
Based on the data from [17], it is possible to calculate the value \(\overline \sigma _{x,y}^ + \), which determines the relaxation of transformation stresses at the pore edge, and subsequently compute the values of Е1(с) and Е2(с), where с = a/r (with a and r being the half-thickness and radius of the martensite crystal, as shown in Fig. 4). The resulting dependencies, recalculated per unit volume as \(\frac{{{E_1}(c)}}{V}\) and \(\frac{{{E_2}(c)}}{V}\), are illustrated in Fig. 5. It becomes evident that the shape of the nucleus does not significantly impact the obtained data, although the elastic energy during nucleation from a pore decreases more markedly in the case of a rhomboidal cross-section (Fig. 5, curve 1ʹ). Experimentally, such rhomboidal-shaped plates growing from pores have been observed (Fig. 1). Therefore, all subsequent relationships refer to a plate with a rhomboidal cross-section.
Fig. 5. Dependencies \(\frac{{{E_1}(c)}}{V}\), \(\frac{{{E_2}(c)}}{V}\) and \(\frac{{{E_1}(c)}}{{{E_2}(c)}}\) for plates |
Within the range of 0.1 ≤ с ≤ 0.4 the curves \(\frac{{{E_1}(c)}}{V}\) and \(\frac{{{E_2}(c)}}{V}\) assuming с2 \( \ll \) 1 with an accuracy of ε < 5 %, are described by linear equations of the form
| \[\frac{{{E_1}(c)}}{V} = \frac{{\mu \gamma _x^2}}{{\pi (1 - v)}}\left( {1.188c + 0.03} \right){\rm{ 1/m}},{\rm{J/}}{{\rm{m}}^{\rm{3}}};\] | (6) |
| \[\frac{{{E_2}(c)}}{V} = \frac{{\mu \gamma _x^2}}{{\pi (1 - v)}}\left( {0.746c + 0.019} \right){\rm{ 1/m}},{\rm{J/}}{{\rm{m}}^{\rm{3}}}.\] | (7) |
Using the traditional approach [18], the value of the “classical” nucleation barrier can be determined as follows:
| \[\begin{array}{c}{F^*} = \frac{{32}}{{27}}\frac{{{\sigma ^2}A'}}{{{{\left( {\Delta {f^{\alpha \to \gamma }} - {A^*}} \right)}^2}}};\\A' = \frac{{dE(c)/V}}{{dc}};\\{A^*} = \left( {\frac{{E(c)}}{V}} \right) - A'.\end{array}.\] | (8) |
From equation (8), the Ms point for nucleation at the pore surface (denoted as Т2 in this context) can be derived if Т1 is known – the Ms temperature during martensite formation within the austenite volume between pores:
| \[\Delta {f^{\alpha \to \gamma }}({T_2}) = \sqrt {\frac{{{{A'}_1}}}{{{{A'}_2}}}} \left( {\Delta {f^{\alpha ' \to \gamma }}({T_1}) - A_1^*} \right) + A_2^*.\] | (9) |
where \({A'_1}\) and \(A_1^*\) correspond \({A'_2}\) and \(A_2^*\), respectively, in the case of nucleation within the austenite volume between the pores (index 1) and at the free surface of the pores (index 2).
For the values μ = 8·1010 N/m2; v = 0.23; γx = 0.18; σ = 0.2 N/m2; Δf\(^{\rm{α′ → γ}}\)(Т1) = 1.75·108 J/m3 [18] for steels with a carbon concentration of 0.4 ‒ 1.2 %, the increase in Т2 over Т1 is approximately 75 K.
The following conclusions can be drawn from these results:
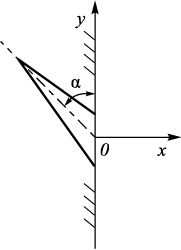
1. Stress relaxation at the pore surface (Fig. 5) is minimal compared to the scenario where the crystal is inclined relative to the surface (Fig. 6), where the martensite start temperature would be even higher. The potential increase in the Ms point depends on the angle α (Fig. 6), with the maximum being the equilibrium temperature of the transforming phases. As the angle varies from 90 to 0°, the number of habit planes changes by a factor of sin α. In the case of a spherical pore, any angle may be equally probable; thus, as α decreases, the probability of nucleation from the pore diminishes according to the sin α function. The modeling results show good agreement with experimental data: in steels with a carbon concentration of 0.4 – 1.2 % and a porosity of approximately 30 %, the Ms point increases by about 100 °С [2; 19].
Fig. 6. Arrangement of two-dimensional plate at angle α |
2. As observed from equation (9), the increase in Т2 over Т1 for Fe – 0.4 ÷ 1.2 % C steels is independent of alloy composition, which is also experimentally confirmed [2; 20].
3. The well-known linear dependence of the Ms temperature of sintered steels on porosity can be attributed to the approximately linear increase in the specific free surface area of the material. The accuracy of experimental determination of the Ms temperature allows it to be fixed only when more than 1 % of the α′-phase volume fraction appears, thereby clearly illustrating the dependence of Ms on porosity.
4. Experimental data indicate that for crystals formed at an angle of 90° from the pore, the maximum ratio of half-thickness to radius was с ≤ 0.23. Theoretically, the maximum value is 0.25.
Conclusions
The calculation results indicate that martensite crystals oriented at a 90° angle to the pore have the highest probability of nucleation, with the ratio of their half-thickness to radius approaching the maximum possible value. It has been demonstrated that the difference in the martensite start temperature between nucleation at the pore surface and nucleation between pores is independent of the alloy composition. The well-known linear dependence of the martensite start temperature on porosity is determined by the increase in the specific free surface area. Therefore, in sintered porous steels, porosity is an unavoidable factor that raises the Ms temperature. Segregation effects, which arise due to incomplete homogenization during sintering or during austenitization prior to quenching, can be excluded.
References
1. Gurevich Yu.G., Rakhmanov V.I. Heat Treatment of Powder Steels. Moscow: Metallurgiya; 1985:81.
2. Ermakov S.S. Heat Treatment of Powder Steel Parts. Leningrad: LDNTP; 1981:24.
3. Egorov M.S., Egorova R.V., Tsordanidi G.G. Formation of structural features of powder materials during cooling after heat treatment. Safety of Technogenic and Natural Systems. 2022;(2):69–75. (In Russ.). https://doi.org/10.23947/2541-9129-2022-2-69-75
4. Pustovoit V.N., Dolgachev Yu.V., Kornilov Yu.A., Sorochkina O.Yu. Unstable of the crystalline lattice before martensite transformation and the influence of the external magnetic field under these conditions. Vestnik Donskogo gosudarstvennogo tekhnicheskogo universiteta. 2009;9(2(41)):238–248. (In Russ.).
5. Egorov M.S., Egorova R.V. Determination of mechanical properties of sintered dispersion-strengthened iron-based alloys depending on sintering conditions. Safety of Technogenic and Natural Systems. 2022;(2):76–83. (In Russ.). https://doi.org/10.23947/2541-9129-2022-2-76-83
6. Antsiferov V.N., Gilev V.G. Studies of the structure of martensite in sintered carbon steels. Izvestiya. Ferrous Metallurgy. 1982;25(5):99–102. (In Russ.).
7. Antsiferov V.N., Grevnov L.M. Structure of Powder Steels. Ekaterinburg: UB RAS; 2011:219.
8. Antsiferov V.N. Formation of fulleren-content structure in process of powders iron-graphite compound sintering. Perspektivnye materialy. 2009;(6):77‒82. (In Russ.).
9. Umemoto M., Furuhara T., Tamura I. Effects of austenitizing temperature on the kinetics of bainite reaction at constant austenite grain size in Fe-C and Fe-Ni-C alloys. Acta Metallurgica. 1986;34(11):2235–2245. https://doi.org/10.1016/0001-6160(86)90169-0
10. Morsdorf L., Kashiwar A., Kübel C., Tasan C.C. Carbon segregation and cementite precipitation at grain boundaries in quenched and tempered lath martensite. Materials Science and Engineering: A. 2023;862:144369. https://doi.org/10.1016/j.msea.2022.144369
11. Butler E.P., Burke M.G. Chromium depletion and martensite formation at grain boundaries in sensitised austenitic stainless steel. Acta Metallurgica. 1986;34(3):557–570. https://doi.org/10.1016/0001-6160(86)90091-X
12. Zhang Y., Zhan D., Qi X., Jiang Z. Austenite and precipitation in secondary-hardening ultra-high-strength stainless steel. Materials Characterization. 2018;144:393‒399. https://doi.org/10.1016/j.matchar.2018.07.038
13. Roitburd A.L. Theory of heterophase structure formation during phase transformations in solid state. Uspekhi fizicheskikh nauk. 1974;113:69–104. (In Russ.).
14. Olson G.B., Cohen M. Interphase-boundary dislocations and the concept of coherency. Acta Metallurgica. 1979;27(12): 1907–1918. https://doi.org/10.1016/0001-6160(79)90081-6
15. Khachaturyan A.G. Theory of Structural Transformations in Solids. Courier Corporation, 2008:576.
16. Rabotnov Yu.N. Mechanics of Deformable Solids. Moscow: Nauka; 1988:712.
17. Anderson P.M. Hirth J.P., Lothe J. Theory of Dislocations. Cambridge University Press; 2017:699.
18. Kaufman L., Cohen M. Thermodynamics and kinetics of martensitic transformations. Progress in Metal Physics. 1958;7:165–246. https://doi.org/10.1016/0502-8205(58)90005-4
19. Danninger H., Gierl C., Mühlbauer G., Gonzalez M.S., Schmidt J., Specht E. Thermophysical properties of sintered steels – Effect of porosity. International Journal of Powder Metallurgy. 2011;47(3):31–42.
20. Ternero F., Rosa L.G., Urban P., Montes J.M., Cuevas F.G. Influence of the total porosity on the properties of sintered materials – A review. Metals. 2021;11(5):730. https://doi.org/10.3390/met11050730
About the Authors
V. N. PustovoitRussian Federation
Viktor N. Pustovoit, Dr. Sci. (Eng.)., Prof. of the Chair of Materials Science and Metals Technology
1 Gagarina Sqr., Rostov-on-Don 344002, Russian Federation
Yu. V. Dolgachev
Russian Federation
Yurii V. Dolgachev, Cand. Sci. (Eng.)., Assist. Prof. of the Chair of Materials Science and Metals Technology
1 Gagarina Sqr., Rostov-on-Don 344002, Russian Federation
M. S. Egorov
Russian Federation
Maksim S. Egorov, Cand. Sci. (Eng.)., Assist. Prof., Head of the Chair of Materials Science and Metals Technology
1 Gagarina Sqr., Rostov-on-Don 344002, Russian Federation
Yu. M. Vernigorov
Russian Federation
Yurii M. Vernigorov, Dr. Sci. (Eng.)., Prof. of the Chair of Physics
1 Gagarina Sqr., Rostov-on-Don 344002, Russian Federation
Review
For citations:
Pustovoit V.N., Dolgachev Yu.V., Egorov M.S., Vernigorov Yu.M. Influence of inhomogeneities in chemical composition and porosity of sintered steel on development of martensitic transformation. Izvestiya. Ferrous Metallurgy. 2024;67(4):417-423. https://doi.org/10.17073/0368-0797-2024-4-417-423