Determination of longitudinal stability of strip in rolling cage – non-drive dividing device system

Modern realities are characterized by the active growth in industrial and civil construction. Advanced construction technologies increasingly rely on the use of prefabricated structures made of reinforced concrete and metal products [1 – 3]. The constantly rising demand for construction metal products necessitates solutions that offer a short payback period, low costs for production re-equipment, and a significant increase in productivity. The rolling – separation technology meets all these requirements [4; 5]. Currently, the rolling – separation technology is developing in two directions, distinguished by where the longitudinal dividing occurs: either within the rolls of the rolling mill, which simultaneously forms and divides the articulated profile, or in a separate stand-alone non-driven dividing device. On most modern rolling mills, the second method is preferred, as separating the operations of forming the articulated profile and subsequent longitudinal separation in a separate stand-alone non-driven device significantly simplifies equipment setup [6 – 9]. However, this arrangement can lead to a potential loss of natural longitudinal stability if the distance between the rolling mill and the non-driven dividing device is chosen incorrectly. Currently, this issue is addressed through trial and error, which results in increased defective products and unforeseen downtime of the primary rolling equipment.

The use of 3D simulation methods does not allow for the assessment of the permissible distance that ensures natural longitudinal stability [10]. To evaluate the risk of losing longitudinal stability of the strip and to determine the critical distance between the rolling mill and the non-driven dividing device, a dependency obtained using the well-known Euler’s formula [11] is proposed:

\[{l_{\max }} = \frac{{\pi \sqrt {Ei_{\min }^2} }}{{\sqrt {{\sigma _2}} k}},{\rm{at  }}\frac{{{\sigma _2}}}{{{\sigma _s}}} \le 1,\]

where l_max is the maximum permissible distance between the rolling mill, which forms the articulated profile, and the non-driven dividing device, ensuring longitudinal stability; Е is the modulus of elasticity of the first kind, MPa; k is the coefficient of length reduction; i_min is the minimum radius of the section inertia; σ₂ is the support stress necessary for longitudinal division by the non-driven dividing device; σ_s is the resistance to deformation of the material being divided.

As can be seen from the presented dependency, the magnitude of the maximum permissible distance depends on the support stress necessary for longitudinal separation, the shape, and the area of the cross-section of the articulated profile, which are characterized by the minimum radius of inertia, the modulus of elasticity of the first kind, and the coefficient of length reduction. Among the factors considered, the coefficient of length reduction has a significant impact, varying from 0.5 to 2.0 depending on the nature of the clamping [11].

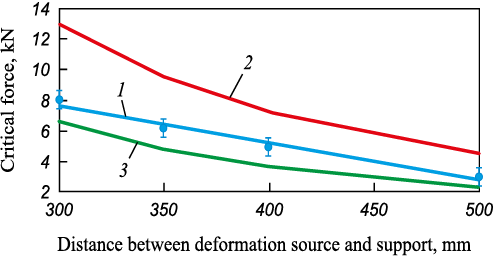
To determine the coefficient of length reduction during the implementation of the rolling – separation process, laboratory experiments were conducted. These experiments compared the critical force corresponding to the moment of loss of stability, obtained both theoretically using Euler’s equation and experimentally. The experimental and theoretical data obtained with coefficients of length reduction of 0.5 and 0.7 are shown in the figure.

According to the obtained data, when determining the natural longitudinal stability of the strip in the rolling mill – non-driven dividing device system, a coefficient of length reduction equal to 0.7 is required to achieve values closer to the experimental data. With a coefficient of length reduction of 0.7, the calculated data are 10 – 15 % less than the experimental data. In practical use, this provides a margin of safety when determining the permissible distance in the rolling mill–non-driven dividing device system.

Conclusions

A dependency has been derived that enables the estimation of the maximum permissible distance between the rolling mill stand and the non-driven dividing device, ensuring the longitudinal stability of the strip during the implementation of the rolling–separation technology. Experimentally, it has been established that the length conversion coefficient for the rolling–separation technology using a non-driven dividing device should reasonably be taken as 0.7.