Kinetics of deformation fronts during serrated Lüders deformation in α-iron at high temperature

Introduction

At room temperature, deformation of most BCC metals containing small amounts of interstitial elements is accompanied by the formation of a Chernov–Lüders band, which propagates monotonically across the yield plateau during tension [1 – 4]. The propagation behavior of the Lüders band can vary depending on grain size, temperature, applied stress, and strain rate. The band expands uniformly across the yield plateau, with all deformation concentrated at its boundaries, or deformation fronts, at any given moment. The velocities of front movement are proportional to the velocity imposed by the loading device. According to the autowave concept [5 – 7], the Chernov–Lüders band front represents an autowave switch that transitions from a metastable elastically deformable state to a stable plastically deformable state [8; 9]. However, within the blue brittleness temperature range for mild steels (423 – 510 K) [10 – 12], where dislocation movement is influenced by dynamic strain aging, the propagation of the Lüders band is characterized by discrete flow. In [13], it was established that within the temperature range of 393 – 503 K in ARMCO iron, the stationary kinetics of Lüders front movement is replaced by serrated behavior. The temperature at which Lüders deformation becomes serrated increases with increasing deformation rate. On the serrated yield plateau, the discretely propagating Lüders band front represents an autowave of localized plasticity excitation. Notably, front movement in this case only occurs during the stress relaxation process associated with serration. This raises a question about the nature of dependence of the local deformation rate in front region on the applied stress during the serrated process.

This study is dedicated to establishing the kinetic regularities of deformation front propagation during serrated Lüders deformation in α-iron at elevated temperatures.

Materials and methods

The material used for the study was ARMCO iron with the following composition (wt. %): C 0.025; Si 0.05; Cu 0.05; Mn 0.035; S 0.025; P 0.015; Fe – remainder. Test samples in the form of double-sided blades were laser-cut from hot-rolled sheet with a thickness of 1.5 mm. The working area of the sample was 50×10 mm. To standardize the stress and structural states before testing, the samples were annealed in a vacuum according to the following regime: 1233 K for 1 h, followed by cooling with the furnace to room temperature.

The prepared samples were subjected to uniaxial tension using an LFM-125 testing machine at speeds ranging from 0.02 to 10 mm/min. Tests were conducted at temperatures ranging from 296 to 503 K. The STE-12H furnace (Walter + Bai) with independent temperature control in three zones was used. The sample temperature was measured using three thermocouples installed along the sample axis at a distance of 20 mm from each other.

Analysis of the kinetics of Lüders deformation fronts was performed using digital image correlation [14; 15] and digital statistical speckle photography [16; 17]. To form the speckle structure, the sample was illuminated with coherent light from a semiconductor laser (635 nm, 15.0 mW). The sample images were captured using a Point Grey FL3-GE-50S5MC digital video camera with a resolution of 2448×2048 pixels at a frame rate of 2 to 25 fps, depending on the stretching speed. Chronograms [18] were constructed from the obtained data arrays, which allowed for the identification of Lüders band nucleation regions and determination of the kinetic characteristics of their fronts.

Results and discussion

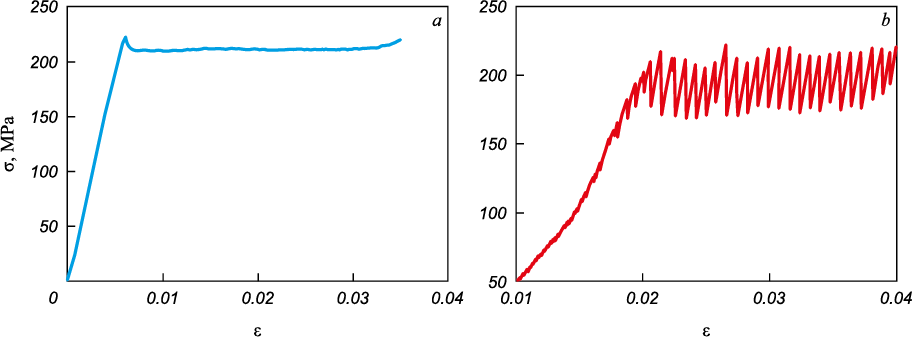
Fig. 1 shows the yield plateaus of the stress-strain curves of ARMCO iron obtained at room temperature and elevated temperatures. At room temperature, the strain curve exhibits a typical tooth and smooth yield plateau characteristic of low-carbon steels. At a test temperature of 423 K and a deformation rate of 6.67·10\(^–\)⁵ s\(^–\)¹, periodic stress jumps occur on the yield plateau.

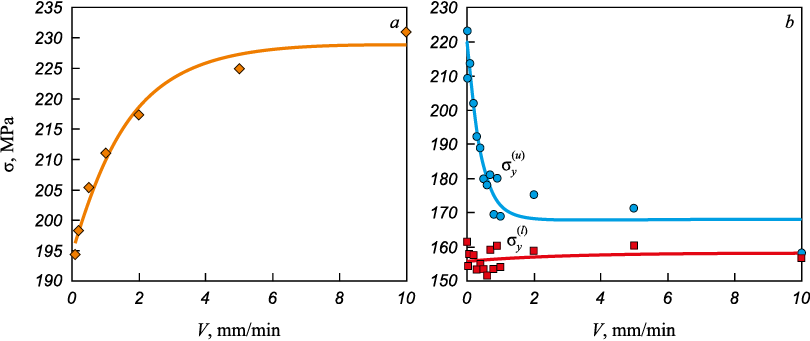
It is known that at temperatures below 393 K, ARMCO iron exhibits normal strain rate sensitivity, meaning that the yield stress on the yield plateau (lower yield strength \(\sigma _y^{(l)}\) ) increases with increasing deformation rate and decrease with increasing temperature [19]. As shown in Fig. 2, a, at room temperature, the lower yield strength increases non-linearly with increasing deformation rate.

Studies in the temperature region of the serrated development of the Lueders strain have shown that with increasing deformation rate, the amplitude of stress jumps decreases, while the stress level \(\sigma _y^{(l)}\), at which the drop occurs remains constant (Fig. 2, b). Thus, in the temperature range of serrated flow, the strain rate sensitivity of the lower yield strength is absent. At the same time, the stress at the onset of the jump (upper yield strength \(\sigma _y^{(u)}\)) monotonically decreases with increasing deformation rate.

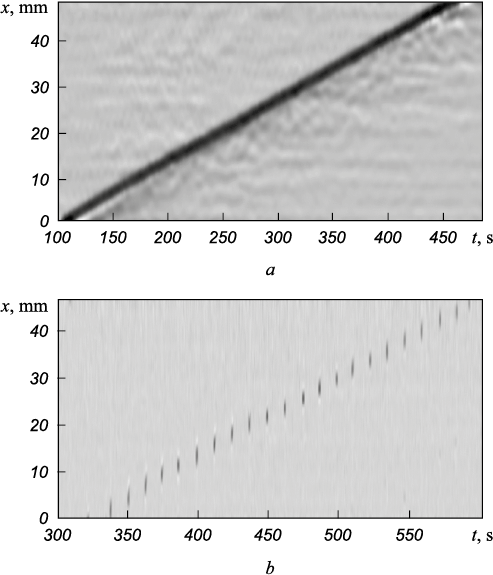
Studies on the nature of deformation localization using digital statistical speckle photography identified that fronts of localized plastic deformation form and move both on the smooth (Fig. 3, a) and serrated (Fig. 3, b) yield plateaus. However, in the former case, the front moves monotonically at a constant velocity V_f, while in the latter case, it moves discretely, only during the stress drop in the serration process.

Based on the fact that the deformation front passes through the entire length of the sample L during the observed yield plateau Δt, then L = V_fΔt. During this time, the sample undergoes elongation expressed as ∆L = V_d∆t (where V_d is the deformation rate set by the loading device). Therefore, the deformation acquired by the sample on the yield plateau can be represented as

From this, it follows that the front velocity and deformation rate are interrelated by the equation V_d = ε_LV_f. If this relationship is normalized by the front width δ, then the relative deformation velocity is expressed as

where t_f is the time of front motion during a jump at a certain velocity V_f.

Thus, the relative deformation velocity \(\dot \varepsilon\) and front velocity V_f must be linearly related if the deformation ε_L at any given time is constant and concentrated at the front. Furthermore, for this equation to hold, the width of the deformation front δ during motion must also remain constant.

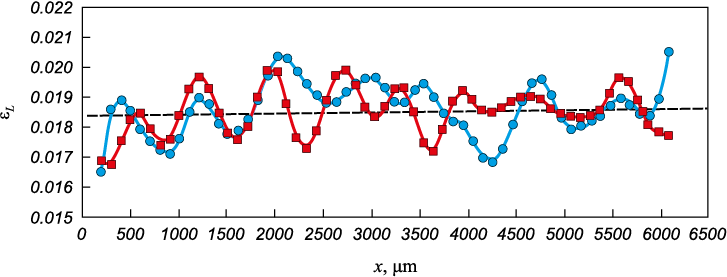
To test the first postulate of ε_L constancy, measurements of marker displacements on the surface of the sample were conducted during deformation on a serrated yield plateau. Markers were applied to the surface of the sample in three rows, spaced 100 μm apart, using a PMT-3M microhardness tester. Two series of images of these markers were then taken before and after deformation using a NEOPHOT-21 optical microscope. Measurements of the distance between the centers of two adjacent markers before deformation (l) and after deformation (l₁) allowed for the determination of the displacement of each marker ∆l = l₁ – l, thus obtaining the displacement field ∆l(x) (where x is the marker coordinate). By numerically differentiating this field, the local deformation at each point was calculated as ε_L = Δl / l. Fig. 4 shows the distribution of ε_L along the length of the sample. The application of the hypothesis of a normally distributed population [20] showed that changes in ε_L are random in nature, with the magnitude being considered constant and its average value being ε_L = 0.0184 ± 0.0003.

As stated in [17], when using the digital statistical speckle photography method to visualize deformation fronts, the brightness of the front image is proportional to the deformation within it. From this, the average width of the front δ can be determined. Measurements for fronts moving during all jumps (Figs. 1, b and 3, b) showed that their width is constant and equal to 105 ± 7 μm. Thus, the second postulate of front width constancy is also fulfilled, and equation (2) can be used to investigate the relationship between local deformation rate and stress in the during a jump.

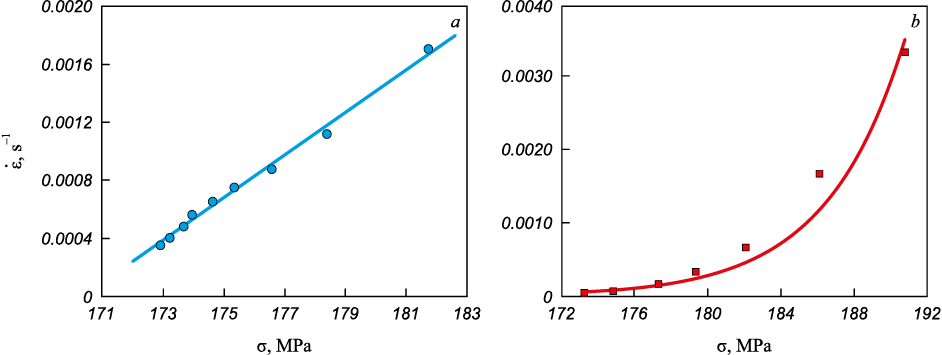
Fig. 5, a shows this dependence. It can be seen that \(\dot \varepsilon\) increases linearly with increasing stress. The correlation coefficient of the interpolating relationship is ρ = 0.99. On the other hand, in the case of a monotonically moving front, based on the correlation relationship (Fig. 2) and equations (1) and (2), the strain rates at the front can be calculated for each \(\sigma _y^{(l)}\)  (Fig. 5, b). It is evident that it cannot be interpolated by a linear function. In other words, the strain rates in the monotonically moving front and the serrated moving front react differently to changes in the stress state.

The reason for this difference may be the change in the deformation autowave mode from the autowave of switching to the autowave of excitation. In [13], it is shown that the kinetics of Lüders front motion in ARMCO iron is indeed controlled by the effect of dynamic strain aging, i.e., the delay time t_w of mobile dislocations at barriers overcome by thermally activated processes, and the time t_a of carbon impurity deposition on these dislocations. At temperatures below 393 K, when t_a \( \gg \)  t_w, front moves monotonically and represents an autowave of localized plasticity switching. In this case, the local strain rate increases non-linearly with stress according to a parabolic law. The discrete nature of the deformation front movement occurs under temperature-rate conditions where t_w and t_a are comparable. The serrated moving deformation front represents an autowave of localized plasticity excitation. In this case, the local strain rate depends linearly on the applied stress.

Conclusion

The deformation accumulated on the serrated yield plateau in α-iron is constant. Under these conditions, the width of the front is also a constant in the first approximation.

The local strain rate during the monotonic movement of the front (296 – 393 K) increases with stress according to a power law. In the case of serrated Lüders deformation (393 – 503 K), the local strain rate is directly proportional to the applied stress.

The difference in front kinetics is determined by the reaction characteristics of active deformable media to external mechanical action and is controlled by the effect of dynamic strain aging.