Scroll to:
Evolution of dislocation structure and phase composition of deformed Al0.3CoCrFeNi high-entropy alloy during heating
https://doi.org/10.17073/0368-0797-2024-2-176-184
Abstract
When choosing compositions of high-entropy alloys, one of the parameters taken into account is thermal stability. The paper considers the structural transformations of the deformed Al0.3CoCrFeNi high-entropy alloy occurring during its annealing. The material was obtained by argon-arc melting with a mixture of pure single-element components. In order to homogenize the structure, the resulting ingot was subjected to thermomechanical processing according to a scheme combining cold rolling with a compression ratio of 50 % and low-temperature annealing (400 °C for 100 h). In the future, the homogenized billet was rolled in a cold state with a compression ratio of 80 %. The structure of the materials was studied directly during heating (in-situ mode) using the method of synchrotron X-ray diffraction. The heating rate of the samples was 20 °C/min, the maximum heating temperature was 1000 °C. The parameters of the alloy dislocation structure (density of screw dislocations, spatial distribution of dislocations) during heating were determined using the modified Williamson–Hall and Warren–Averbach methods. According to the data obtained, the temperature of beginning of formation of a high-entropy phase with a primitive cubic lattice is 560 °C. In the process of heating the material up to this temperature, an increase in density of screw dislocations and formation of a disordered dislocation structure are observed. The nature of change in dislocation density correlates well with the increase in the alloy microhardness. At an initial value of 406 ± 13 HV0.1 (for the deformed material), the microhardness during heat treatment increases up to 587 ± 10 HV0.1 .
Keywords
For citations:
Ivanov I.V., Akkuzin S.A., Safarova D.E., Litovchenko I.Yu., Bataev I.A. Evolution of dislocation structure and phase composition of deformed Al0.3CoCrFeNi high-entropy alloy during heating. Izvestiya. Ferrous Metallurgy. 2024;67(2):176-184. https://doi.org/10.17073/0368-0797-2024-2-176-184
Introduction
Thermal stability is a crucial parameter often considered when selecting compositions for high-entropy alloys (HEAs) [1 – 4]. For HEAs within multicomponent systems, the formation of both ordered and disordered crystalline phases is typical. Disordered phases are characterized by a random distribution of atoms within the unit cell, typically exhibiting a face-centered cubic (FCC) or body-centered cubic (BCC) lattice, occupying the largest fraction of the alloy volume [5]. However, during melting and subsequent heat treatment of HEAs, the formation of ordered phases with a primitive cubic lattice is possible [6]. Undoubtedly, the formation of such phases leads to changes in the properties of the alloys.
Among the numerous known compositions of HEAs, the AlxCoCrFeNi system is often highlighted [7 – 11]. The peculiarity of alloys within this system lies in the ability to control the phase composition of the alloy by varying the aluminum content. For instance, at x = 0.3, the alloys’ structure consists solely of the BCC phase. Within the range of x values from 0.3 to 0.6, a second phase with an FCC lattice forms alongside the BCC phase in the alloy’s structure. Increasing the parameter x to values of 0.6 – 2.0 is accompanied by the formation of a single-phase FCC structure.
Experimental studies and thermodynamic calculations confirm the correspondence of the structural and phase state to the indicated composition ranges of high-entropy alloys [12]. However, it is known that the formation of additional phases in alloys of the AlxCoCrFeNi system can be significantly influenced by pre-thermo-mechanical processing. For instance, plastic deformation of alloys with x equal to 0.3, 0.6, and 0.9 at 930 °C is accompanied by the precipitation of AlNi particles along grain boundaries [13]. Additionally, research indicates that the formation of an intermetallic phase in AlxCoCrFeNi alloys can occur during dry friction at 900 °C. Deformation and annealing processes result in the formation of ordered high-entropy phases. For example, plastic deformation of the Al0.3CoCrFeNi alloy with a compression degree of 20 % followed by annealing at 550 °C leads to the formation of a phase with an L12 structure (characterized by a primitive cubic lattice). Increasing the annealing temperature to 700 °C is accompanied by the formation of the AlNi intermetallic and B2 phases, both possessing a primitive cubic lattice. Furthermore, the B2 phase is observed after annealing of samples deformed by the high-pressure torsion method [16]. Cold rolling of the Al0.3CoCrFeNi alloy with a compression degree of 50 % followed by annealing at 800 °C leads to the formation of the B2 phase [17]. The significant influence of annealing temperature on the mechanical properties of deformed HEA blanks is also noted [17].
From the analysis of available publications, several conclusions can be drawn. Firstly, alloys of the AlxCoCrFeNi system are characterized by the formation of not only high-entropy disordered phases but also multi-component phases with ordered structures. Secondly, the phase composition of these materials is largely determined by the scheme and modes of thermomechanical processing. The combination of plastic deformation and high-temperature annealing promotes the formation of ordered high-entropy phases. By varying the parameters of temperature-force exposure, it is possible to change the temperature at which the ordered phases begin to precipitate. Finally, a number of studies indicate the possibility of changing the mechanical properties of high-entropy alloys depending on the annealing temperature.
The questions regarding the thermal stability of HEAs, the formation of ordered phases in them, and changes in their mechanical properties depending on temperature effects are important not only for controlling the structure and properties of the final product but also for understanding the conditions under which this product can function. While acknowledging the significance of this issue, it should be noted that there is a lack of experimental data revealing the peculiarities of the formation of new phases in the analyzed HEAs under deformation and thermal conditions. In this work, the method of synchrotron X-ray diffraction in situ was employed to analyze the changes in the structure of the deformed Al0.3CoCrFeNi alloy during heating. This method, combined with profile analysis of recorded diffraction patterns, allowed for the calculation of lattice parameter changes, identification of the temperature at which the formation of ordered high-entropy phase begins, and estimation of the density of dislocations during material heating. Additionally, the structure of the materials was investigated using transmission electron microscopy, and the hardness of the samples was evaluated using the Vickers method.
Materials and methods
A high-entropy alloy ingot Al0.3CoCrFeNi was produced by argon arc melting of pure elemental components. The melting process took place in a Bühler ArcMelter AM furnace at an argon pressure of 2·10\(^–\)2 bar (2·103 Pa). To ensure a homogeneous chemical composition, the material underwent ten cycles of remelting. Additional thermomechanical treatment of the alloy was also conducted for the same purpose. The resulting ingot underwent cold rolling with a reduction degree of 50 % and was held at 400 °C for 100 h. This thermal treatment regime was employed to prevent the formation of ordered phases in the alloy structure [18].
The prepared billet was utilized for investigations aimed at studying the influence of heating temperature on the structural and phase transformations of the alloy deformed by cold rolling. The total reduction degree of the billet, amounting to 80 %, was achieved through multiple passes. Each pass involved a 2 % reduction in thickness relative to the initial billet thickness. Samples cut from the cold-deformed sheet were placed in a Bähr DIL 805 A/D dilatometer furnace and heated at a rate of 20 °C/min, with the maximum heating temperature reached 1000 °C.
The analysis of the material structure during heating was conducted using the in-situ synchrotron X-ray diffraction method. The investigations were carried out at the P07 (“High Energy Materials Science”) beamline of the DESY: PETRA III source in Hamburg. The wavelength of the X-ray radiation used was 0.014235 nm, corresponding to a photon energy of 87.1 keV. A 2D scintillation detector PerkinElmer XRD 1621 with a resolution of 2048×2048 pixels and an area of 409.6 mm2 was employed to record the diffraction patterns, with the distance from the sample to the detector being 1.05 m. The diffraction patterns were recorded in transverse direction and were converted into one-dimensional form by azimuthal integration using the pyFAI library [19].
To perform profile analysis, the one-dimensional diffraction patterns were described by the following function:
| \[{I_{{\rm{pattern}}}}(2\theta ) = \sum\limits_{i = 1}^{10} {{I_i}(2\theta )} + \sum\limits_{j = 0}^7 {{a_j}{{(2\theta )}^j}} .\] | (1) |
The first sum in Eq. (1) determines the contribution of ten diffraction maxima to the intensity, while the second represents the 7\(^\rm{th}\) order polynomial describing the background of the diffraction pattern. In turn, the profile of each of the diffraction maxima was described by a pseudo-Voight function as follows:
| Ii (2θ) = I0 [η L(2θ) + (1 – η) G(2θ)], | (2) |
where I0 is the maximum intensity of diffraction maximum; η is the contribution of the Lorentz function; L(2θ) and G(2θ) are Lorentz and Gaussian functions, respectively, defined as:
| \[L(2\theta ) = \frac{{{{[0.5\beta (1 - A)]}^2}}}{{{{[0.5\beta (1 - A)]}^2} + {{(2\theta - 2{\theta _0})}^2}}},\] | (3) |
| \[G(2\theta ) = \exp \left\{ {\frac{{ - \pi {{(2\theta - 2{\theta _0})}^2}}}{{{{\left[ {0.5\beta (1 - A)\sqrt {\frac{\pi }{{\ln 2}}} } \right]}^2}}}} \right\},\] | (4) |
where 2θ0 is the angular position corresponding to the maximum intensity of the peak; β is the full width at half maximum of the diffraction peak; A is the asymmetry parameter of the diffraction peak (–1 ≤ A ≤ 1).
The parameters of the dislocation structure (density of screw dislocations, spatial arrangement of dislocations) corresponding to a specific stage of alloy heating were determined using modified Williamson–Hall and Warren–Averbach methods. A detailed description of these methods is presented in [20 – 23].
In addition to experiments analyzing the structure using synchrotron X-ray radiation, a series of samples was prepared to evaluate the microhardness of cold-deformed HEA after heating to 100 – 900 °C (in intervals of 50 °C), including 875 and 900 °C. The materials were analyzed using the Vickers method on a semi-automatic hardness tester WolpertGroup 402MVD. The load on the four-sided diamond indenter was 0.98 N, with a dwell time under load of 10 s. The fine structure of samples thermally treated at 550, 650, and 900 °C was examined using a transmission electron microscope JEOL JEM-2100 at an accelerating voltage of 200 kV.
Results and discussion
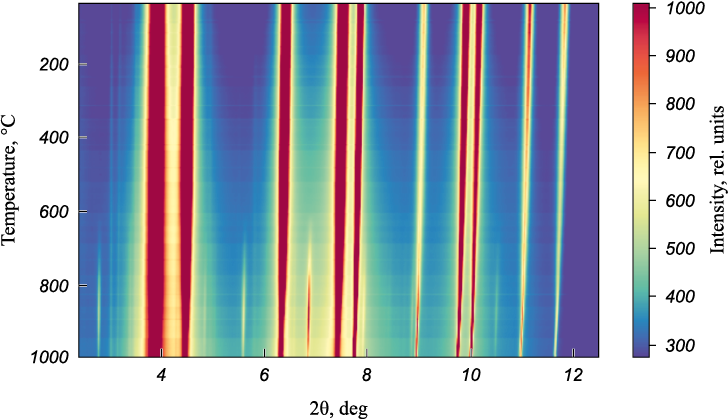
In previous publications, various data on the characteristics of phase transformations occurring during the heating of Al0.3CoCrFeNi alloy have been presented. It has been noted that one of the factors determining the temperature at which ordered phases start to precipitate is the degree of pre-deformation of the material. For example, in [17], it was demonstrated that the temperature at which the B2 phase starts to form in Al0.3CoCrFeNi alloy, cold-rolled to 50 %, falls within the range of 600 – 800 °C. However, the exact value of this temperature could not be determined accurately in the ex-situ experiment. An undeniable advantage of the in-situ approach implemented in this study is the ability to precisely determine the temperatures of phase and structural transformations occurring during the heating of the alloy. Fig. 1 displays a diffraction pattern corresponding to the heating process of the cold-rolled Al0.3CoCrFeNi alloy. Throughout the entire temperature range, diffraction peaks of the FCC phase are observed. However, starting from around 600 °C, peaks of a phase with a primitive cubic lattice emerge. To more accurately determine the temperature at which it starts to form, an analysis of the intensity change of the (310) diffraction peak was conducted (Fig. 2).
Fig. 1. X-ray diffraction pattern of heating of the cold rolled Al0.3CoCrFeNi alloy |
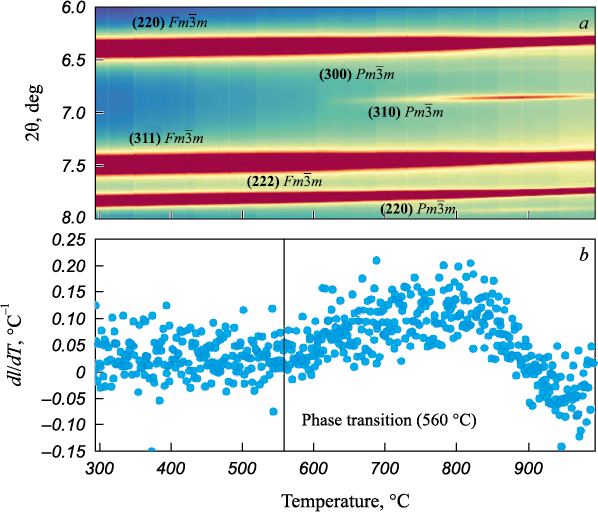
The data presented indicate a non-monotonic change in the intensity of the peak (310) of the phase with a primitive cubic lattice (Fig. 2, a). A characteristic feature of this parameter is its gradual increase with temperature followed by a decrease. The analyzed phase begins to form at 560 °C (Fig. 2, b).
Fig. 2. Change in intensity of diffraction maxima of the disordered and ordered phases |
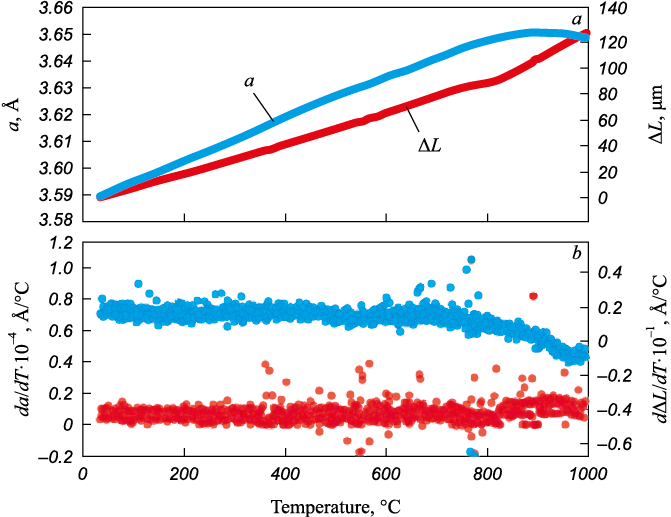
Figure 3 illustrates the results of changes in the material lattice parameter and linear expansion of the sample. Upon heating to approximately 750 °C, the rate of change of both parameters becomes close to linear. A weakly pronounced change in the relationship between the magnitude ΔL and the heating temperature is observed in the temperature range of 450 – 600 °C (Fig. 3, b). This observed effect may be explained by the restructuring of the dislocation structure of the alloy. Upon heating the alloy to above 850 °C, the lattice parameter growth rate increases from 0.07·10\(^–\)4 to 0.125 Å/°C. In the temperature range of 750 – 900 °C, the rate of growth of the parameter ΔL gradually decreases, and in the temperature interval of 900 – 1000 °C, a sample compression effect is manifested.
Fig. 3. Change in the lattice parameter a ( |
Fig. 4 displays the results of profile analysis of experimentally recorded diffraction patterns. Using modified Williamson–Hall and Warren–Averbach methods, the values of screw dislocation density (ρscrew ) and Wilkens parameter (M) were calculated. The parameter M characterizes the spatial configuration features of dislocations. A decrease in M indicates the formation of dislocation walls in the alloy, while an increase in M is a sign of the formation of a disordered dislocation structure. According to the obtained data, up to the onset of ordered phase precipitation (560 °C), there is a simultaneous increase in dislocation density and disordering of the dislocation structure.
Fig. 4. Change in density of screw dislocations ( |
The change in dislocation density correlates well with the increase in microhardness of the analyzed samples. In the initial state (before heating), the microhardness of the cold-deformed sample is 406 ± 13 HV0.1 . The maximum microhardness value at 587 ± 10 HV0.1 is recorded in samples thermally treated at 550 – 600 °C. According to the results of profile analysis, at these temperatures, the values of dislocation density are also at their maximum level. As the temperature is further increased, the dislocation density and microhardness level decrease to 395 ± 16 HV0.1 .
The authors of [23] have previously discussed the changes in structure and properties of the Al0.3CoCrFeNi alloy depending on the heat treatment temperature. In [24], it was noted that plastic deformation followed by annealing of the high-entropy alloy Al0.3CoCrFeNi leads to the the formation of an ordered phase with a primitive cubic lattice on subgrain boundaries or in areas of high local defect density. However, the issue regarding the increase in dislocation density during the heating process of high-entropy alloys has not been discussed in publications before and requires further research.
Analysis of Fig. 4 allows us to conclude that exceeding the temperature values corresponding to the onset of ordered phase precipitation is accompanied by a decrease in both dislocation density and the Wilkens parameter. This fact indicates the activation of processes associated with polygonization and recrystallization of the alloy structure. The results of the research conducted using transmission electron microscopy (Fig. 5) also indicate the development of recrystallization processes. Analysis of the presented images shows an increased degree of structural defects in the material in the cold-deformed state (Fig. 5, a), as well as after heating to 550 and 650 °C (Fig. 5, b, c).
Fig. 5. Results of transmission electron microscopy of Al0.3CoCrFeNi alloy after cold rolling (a) |
Despite the fact that, according to synchrotron radiation diffraction data, the formation of the phase with a primitive cubic lattice begins at 560 °C, even after heating to a temperature of 650 °C, no particles of this phase were detected using transmission electron microscopy (Fig. 5, c). This can be explained by the fact that at the initial stage of particle formation, the analyzed phase particles are small in size and are separated from the original matrix in such a way that they are not visible using diffraction contrast. However, in samples thermally treated at 900 °C, particles of the ordered phase are clearly visible (Fig. 5, d).
Thus, the results of the research conducted using transmission electron microscopy correspond to the experimental data obtained during X-ray structural analysis. The analysis carried out in this work indicates that the intensive decrease in dislocation density and the Wilkens parameter (when heating the alloy to 750 °C) (Fig. 4) is due to the onset of recrystallization processes. The observed decrease in linear expansion rate (ΔL) at heating temperatures above 750 °C is likely also related to the development of recrystallization processes and the accompanying annihilation of crystal structure defects. It can be expected that with further increase in temperature, the linear expansion rate of the sample will reach a plateau, and then the material will begin to expand, but at a different rate. A similar effect was observed in a study [25] that examined the structure of friction-welded samples. The experimentally observed deviation of the ΔL – T dependence from linearity by the authors of this work was associated with recrystallization processes and changes in residual stresses. Similar phenomena were also observed in [26; 27].
Conclusions
Using synchrotron X-ray radiation diffraction, it was determined that the temperature at which the formation of a high-entropy phase with a primitive cubic lattice begins in a cold-rolled sample of Al0.3CoCrFeNi alloy is 560 °C.
Heating the deformed alloy to 560 °C is accompanied by an increase in the density of screw dislocations (ρscrew) and an increase in the degree of disorder in the dislocation structure, expressed by the growth of the Wilkens parameter M.
The change in dislocation density correlates with the nature of the change in microhardness of the Al0.3CoCrFeNi alloy. Heating the cold-worked material from room temperature to 600 °C, accompanied by an increase in dislocation density, leads to an increase in microhardness from 406 ± 13 to 587 ± 10 HV0.1 . The decrease in dislocation density that occurs during further annealing at higher temperatures leads to a decrease in the microhardness of the alloy to 395 ± 16 HV0.1 .
Dilatometric analysis of the Al0.3CoCrFeNi alloy indicates a non-linear relationship between the lattice parameter a and the elongation of the sample ΔL with the heating temperature. In the temperature range from 25 to 850 °C, the rate of lattice parameter growth is 0.07·10\(^–\)4 Å/°C and increases to 0.125 Å/°C when heated above 850 °C. An increase in temperature from 750 to 900 °C is accompanied by a gradual decrease in the rate of linear expansion of the sample. In the temperature range of 900 – 1000 °C, compression is observed. This observed effect may be associated with a decrease in the number of defects in the crystal lattice, accompanying the development of recrystallization processes.
References
1. Thirathipviwat P., Song G., Jayaraj J., Bednarcik J., Wendrock H., Gemming T., Freudenberger J., Nielsch K., Han J. A comparison study of dislocation density, recrystallization and grain growth among nickel, FeNiCo ternary alloy and FeNiCoCrMn high entropy alloy. Journal of Alloys and Compounds. 2019;790:266–273. https://doi.org/10.1016/j.jallcom.2019.03.052
2. Karati A., Guruvidyathri K., Hariharan V.S., Murty B.S. Thermal stability of AlCoFeMnNi high-entropy alloy. Scripta Materialia. 2019;162:465–467. https://doi.org/10.1016/j.scriptamat.2018.12.017
3. Pacheco V., Lindwall G., Karlsson D., Cedervall J., Fritze S., Ek G., Berastegui P., Sahlberg M., Jansson U. Thermal stability of the HfNbTiVZr high-entropy alloy. Inorganic Сhemistry. 2019;58(1):811–820. https://doi.org/10.1021/acs.inorgchem.8b02957
4. Bataeva Z.B., Ruktuev A.A., Ivanov I.V., Yurgin A.B., Bataev I.A. Review of alloys developed using the entropy approach. Obrabotka metallov (Metal Working and Material Science). 2021;23(2):116–146. (In Russ.). https://doi.org/10.17212/1994-6309-2021-23.2-116-146
5. Gromov V.E., Konovalov S.V., Ivanov Yu.F., Osintsev K.A. Structure and Properties of High-Entropy Alloys. Berlin: Springer; 2021;107:110. https://doi.org/10.1007/978-3-030-78364-8
6. Ivanov I.V., Yurgin A.B., Nasennik I.E. Kuper K.E. Residual stress estimation in crystalline phases of high-entropy alloys of the AlxCoCrFeNi system. Obrabotka metallov (Metal Working and Material Science). 2022;23(2):116–146. (In Russ.). http://dx.doi.org/10.17212/1994-6309-2022-24.4-181-191
7. Wang W.-R., Wang W.-L., Yeh J.-W. Phases, microstructure and mechanical properties of AlxCoCrFeNi high-entropy alloys at elevated temperatures. Journal of Alloys and Compounds. 2014;589:143–152. https://doi.org/10.1016/j.jallcom.2013.11.084
8. Osintsev K., Konovalov S., Gromov V., Panchenko I., Chen X. Phase composition prediction of Al-Co-Cr-Fe-Ni high entropy alloy system based on thermodynamic and electronic properties calculations. Materials Today: Proceedings. 2021;46-2:961–965. https://doi.org/10.1016/j.matpr.2021.01.079
9. Osintsev K., Gromov V., Ivanov Y., Konovalov S., Panchenko I., Vorobyev S. Evolution of structure in AlCoCrFeNi high-entropy alloy irradiated by a pulsed electron beam. Metals. 2021;11(8):1228. https://doi.org/10.3390/met11081228
10. Osintsev K.A., Konovalov S.V., Glezer A.M., Gromov V.E., Ivanov Yu.F., Panchenko I.A., Sundeev R.V. Research on the structure of Al2.1Co0.3Cr0.5FeNi2.1 high-entropy alloy at submicro- and nano-scale levels. Materials Letters. 2021;294:129717. https://doi.org/10.1016/j.matlet.2021.129717
11. Gromov V.E., Ivanov Yu.F., Konovalov S.V., Osintsev K.A. Effect of electron beam treatment on the structure and properties of AlCoCrFeNi high-entropy alloy. CIS Iron and Steel Review. 2021;22:72–76. https://doi.org/10.17580/cisisr.2021.02.13
12. Gao M.C., Yeh J.-W., Liaw P.K., Zhang Y. High-Entropy Alloys. Cham: Springer International Publishing; 2016;1:516. https://doi.org/10.1007/978-3-319-27013-5
13. Annasamy M., Haghdadi N., Taylor A., Hodgson P., Fabijanic D. Dynamic recrystallization behaviour of AlxCoCrFeNi high entropy alloys during high-temperature plane strain compression. Materials Science and Engineering: A. 2019; 745:90–106. https://doi.org/10.1016/j.msea.2018.12.102
14. Joseph J., Haghdadi N., Shamlaye K., Hodgson P., Barnett M., Fabijanic D. The sliding wear behaviour of CoCrFeMnNi and AlxCoCrFeNi high entropy alloys at elevated temperatures. Wear. 2019;428-429:32–44. https://doi.org/10.1016/j.wear.2019.03.002
15. Gwalani B., Soni V., Choudhuri D., Lee M., Hwang J.Y., Nam S.J., Ryu H., Hong S.H., Banerjee R. Stability of ordered L12 and B2 precipitates in face centered cubic based high entropy alloys-Al0.3CoFeCrNi and Al0.3CuFeCrNi2 . Scripta Materialia. 2016;123:130–134. https://doi.org/10.1016/j.scriptamat.2016.06.019
16. Tang Q.H., Huang Y., Huang Y.Y., Liao X.Z., Langdon T.G., Dai P.Q. Hardening of an Al0.3CoCrFeNi high entropy alloy via high-pressure torsion and thermal annealing. Materials Letters. 2015;151:126–129. https://doi.org/10.1016/j.matlet.2015.03.066
17. Ivanov I.V., Emurlaev K.I., Kuper K.E., Safarova D.E., Bataev I.A. Structural transformations during annealing of cold-worked high-entropy alloy Al0.3CoCrFeNi. Izvestiya. Ferrous Metallurgy. 2022;65(8):539–547. (In Russ.). https://doi.org/10.17073/0368-0797-2022-8-539-547
18. Asadikiya M., Yang S., Zhang Y., Lemay C., Apelian D., Zhong Y. A review of the design of high-entropy aluminum alloys: a pathway for novel Al alloys. Journal of Materials Science. 2021;56(21):12093–12110. https://doi.org/10.1007/s10853-021-06042-6
19. Ashiotis G., Deschildre A., Nawaz Z., Wright J.P., Karkoulis D., Piccac F.E., Kieffera J. The fast azimuthal integration Python library: pyFAI. Journal of Applied Crystallography. 2015;48-2:510–519. https://doi.org/10.1107/S1600576715004306
20. Ungár T., Borbély A. The effect of dislocation contrast on X‐ray line broadening: A new approach to line profile analysis. Applied Physics Letters. 1996;69(21):3173–3175. https://doi.org/10.1063/1.117951
21. Ungár T., Tichy G. The effect of dislocation contrast on X‐ray line profiles in untextured polycrystals. Physica Status Solidi (a). 1999;171(2):425–434. https://doi.org/10.1002/(SICI)1521-396X(199902)171: 2<425::AID-PSSA425>3.0.CO;2-W
22. Ungár T., Dragomir I., Révész Á., Borbély A. The contrast factors of dislocations in cubic crystals: the dislocation model of strain anisotropy in practice. Journal of Applied Crystallography. 1999;32(5):992–1002. https://doi.org/10.1107/S0021889899009334
23. Dong W., Zhou Z., Zhang L., Zhang M., Liaw P.K., Li G., Liu R. Effects of Y, GdCu, and Al addition on the thermoelectric behavior of CoCrFeNi high entropy alloys. Metals. 2018;8(10):781. https://doi.org/10.3390/met8100781
24. Dasari S., Sarkar A., Sharma A., Gwalani B., Choudhuri D., Soni V., Manda S., Samajdar I., Banerjee R. Recovery of cold-worked Al0.3CoCrFeNi complex concentrated alloy through twinning assisted B2 precipitation. Acta Materialia. 2021;202:448–462. https://doi.org/10.1016/j.actamat.2020.10.071
25. Khosravi J., Givi M.K.B., Barmouz M., Rahi A. Microstructural, mechanical, and thermophysical characterization of Cu/WC composite layers fabricated via friction stir processing. The International Journal of Advanced Manufacturing Technology. 2014;74:1087–1096. https://doi.org/10.1007/s00170-014-6050-x
26. Boso D.P., Lefik M., Schrefler B.A. Thermal and bending strain on rmNb3rmSn strands. IEEE Transactions on Applied Superconductivity. 2006;16(2):1823–1827. https://doi.org/10.1109/TASC.2005.864255
27. Panigrahi B.B., Dabhade V.V., Godkhindi M.M. Thermal expansion behaviour of nanocrystalline titanium powder compacts. Materials Letters. 2005;59(19-20):2539–2541. https://doi.org/10.1016/j.matlet.2005.03.041
About the Authors
I. V. IvanovРоссия
Ivan V. Ivanov, Cand. Sci. (Eng.), Research Associate of the Research Laboratory of Physical and Chemical Technologies and Functional Materials
20 K. Marksa Ave., Novosibirsk 630073, Russian Federation
S. A. Akkuzin
Россия
Sergei A. Akkuzin, Junior Researcher of the Laboratory of Materials Science of Shape Memory Alloys
2/4 Akademicheskii Ave., Tomsk 634055, Russian Federation
D. E. Safarova
Россия
Dar’ya E. Safarova, MA Student of the Chair “Materials Science in Mechanical Engineering”
20 K. Marksa Ave., Novosibirsk 630073, Russian Federation
I. Yu. Litovchenko
Россия
Igor’ Y. Litovchenko, Dr. Sci. (Phys.-Math.), Assist. Prof., Head of the Laboratory of Materials Science of Shape Memory Alloys
2/4 Akademicheskii Ave., Tomsk 634055, Russian Federation
I. A. Bataev
Россия
Ivan A. Bataev, Dr. Sci. (Eng.), Assist. Prof., Head of the Research Laboratory of Physical and Chemical Technologies and Functional Materials
20 K. Marksa Ave., Novosibirsk 630073, Russian Federation
Review
For citations:
Ivanov I.V., Akkuzin S.A., Safarova D.E., Litovchenko I.Yu., Bataev I.A. Evolution of dislocation structure and phase composition of deformed Al0.3CoCrFeNi high-entropy alloy during heating. Izvestiya. Ferrous Metallurgy. 2024;67(2):176-184. https://doi.org/10.17073/0368-0797-2024-2-176-184
JATS XML