Interaction of cracks with grain boundaries in iron bicrystals

Introduction

Numerous studies have been dedicated to investigating the fracture behavior of iron at the microscopic level. The primary research objective was to ascertain how the fracture processes in the material are influenced by internal structural features such as defects, nanoparticles, and grain sizes [1 – 4], along with the application of various loading schemes involving boundary conditions and loading rates [5], as well as different interatomic potentials [6]. Grain boundaries (GBs) play an important role in initiating and propagating fractures within the material. The interaction between cracks and grain boundaries is determined by several parameters, which can be categorized into two groups [7]. The first group encompasses the type and rate of the applied load, crack parameters, in particular, length and distance from the crack to the grain boundary, which influence stress concentration at the crack tip, serving as a driving force for dislocation emission and motion. The second group comprises grain boundary parameters, defining the resistance level to crack propagation. Two predominant models are commonly employed to describe the interaction between cracks and grain boundaries. The first model, developed and detailed in [8; 9], attributes the resistance of a grain boundary to crack propagation solely to the orientation of an adjacent grain. This orientation determines the positions of slip planes in the second grain and the emission of dislocations in the corresponding slip systems. In the second model [10; 11], the slip plane in the adjacent grain is considered differently. Specifically, the crack must alter the slip plane in the mating grain as it crosses the grain boundary. This model introduces two additional parameters determining the resistance value for crack propagation: the grain boundary surface energy characteristic of different types of grain boundaries and the grain boundary tilt angle concerning the surface.

Crack propagation and fracture represent intricate phenomena involving the rupture of atomic bonds and the emission of dislocations from the crack tip. The linear theory of elasticity posits that stress fields at the crack tip are singular [12]. Atomistic modeling of fracture processes offers a way to eliminate singularity and compute accurate stress fields [13; 14]. In the context of brittle material under loading mode I, we utilized molecular dynamics to calculate stresses, local temperature at the crack tip, and the emission of dislocations from the crack. Previous works [15; 16] demonstrated that the initiation of partial dislocations at the crack tip under shear load is significantly influenced by temperature. Additionally, loading modes I, II, III, or their combinations in an iron single crystal markedly affect crack behavior [13]. However, the plasticity at the crack tip is determined by the crystallographic orientation of the sample.

For the study of fracture evolution in materials with a grain structure, it is crucial to identify specific features of the interaction between cracks and grain boundaries. Experimental investigation of crack interaction in materials with specific grain boundaries is challenging. Molecular dynamics, however, provides an effective method for exploring crack interaction with any grain boundaries. Despite its efficacy, there are limited studies on iron bicrystals, with the notable exception of the work [17]. This study was devoted to the fracture resistance of symmetric tilt grain boundaries in iron bicrystals with a seed crack, revealing an inverse relationship between crack delay time at the grain boundary and the grain boundary energy.

The aim of the present work is molecular dynamics modeling of the peculiarities of interaction between cracks propagating in the brittle mode and tilt boundaries in iron bicrystals under uniaxial tension. We investigated the influence of grain boundaries on the retardation and arrest of propagating cracks, peculiarities of grain boundary migration when interacting with the crack, as well as the special features of changes in the excess atomic volume and stress at the crack tip during its evolution and interaction with grain boundaries in iron bicrystals.

Методы исследования

The simulated iron bicrystals comprised approximately 950,000 atoms and exhibited parallelepiped shapes with edge dimensions of 27×40×10 nm (Fig. 1). In Fig. 1, the edges of the grains on the right consistently followed the directions X [\(1\bar 20\)], Y [210], Z [001]. Notably, the grain on the left side of the bicrystal was subjected to a rotation about the Z-axis, with angles of either 10 or 20°. In the simulated samples, the initial temperature was set at 10 K. Free surfaces were set along the X-axis, and periodic boundary conditions were applied along the Z-axis. Non-deformable grips, consisting of three surface atomic planes with a normal along the Y-axis, were configured and moved in opposite directions along the Y-axis at 2.5 m/s each, simulating uniaxial tension in the sample.

The interatomic interaction in iron was characterized by a multiparticle potential developed within the framework of the Finnis–Sinclair approximation of the embedded atom method [18]. The initial distribution of atomic velocities in the sample conformed to the Maxwell distribution, with the initial direction of atomic velocities determined using a random number generator. The integration step was set at 1 fs. Atomic volumes were computed based on the construction of Voronoi polyhedra. To identify local structural changes in the loaded sample, the Common Neighbor Analysis pattern for each atom was employed [19]. The tilt angle of the local lattice relative to the axis [100] was determined using the Polyhedral Template Matching (PTM) algorithm [20]. Visualization of the simulated crystallite structure was accomplished using the OVITo software [21].

To compute the excess volume at the crack tip, a simulated cylinder with a radius R = 1.2 nm was employed. The crack tip was designated as one of the atoms on the crack surface with the maximum coordinate along the X-axis, and the cylinder’s axis aligned with the Z-axis. To determine the atomic volume at the crack tip, the cylinder was systematically shifted along the X- and Y-axes, covering a range from –R to +R relative to the crack tip atom, with an increment of 0.1R. The total volume of atoms within the cylinder was calculated as the sum of Voronoi cell volumes, and the maximum value was selected. The excess atomic volume was defined as the disparity between the Voronoi cell volume and the equilibrium atomic volume at the given temperature. The average excess volume at the crack tip was computed based on the excess volumes of atoms within the cylinder with the maximum volume.

To calculate grain boundary around each atom, the tilt angle of the local lattice from the X-axis was determined using the PTM algorithm. Atoms deviating from the chosen axis by more than half the value of the grain misorientation angle were considered part of the second grain, while the remaining atoms constituted the first grain. Through the loading process, atoms transitioning from one grain to another were identified. The sample volume (dV) through which the grain boundary migrated relative to its initial position was determined as the total atomic volume of these migrating atoms (Fig. 1, b). The parameter for GB migration in the X-axis direction was determined using the formula: L_GB = dV/S_X where S_X is the cross-sectional area of the sample deformed by the plane perpendicular to the X-axis.

Results of the crack behavior modeling

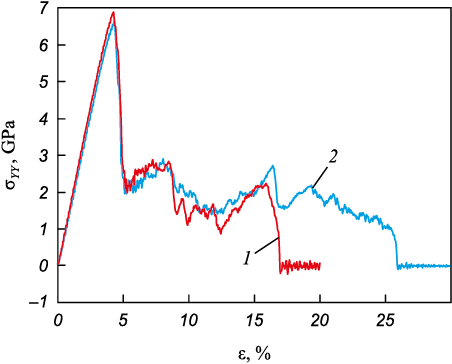
The stress-strain dependencies for bicrystals with misoriented grain boundaries of 10 and 20° are presented in Fig. 2. Notably, the sample with a 20° grain misorientation fractures at a considerably higher strain, approximately 26 %. Despite the difference in fracture strain, the qualitative behavior of the curves for these two grain boundaries is generally similar. The deformation curves in Fig. 2 reveal that the crack propagation process in bicrystals unfolds in four distinct stages. Focusing on the detailed analysis of the fracture evolution in the sample with a 10° grain misorientation, the first stage occurs in the elastic deformation range of 0 – 4.8 %. During this stage, the seed crack remains stationary, and stresses increase linearly, reaching a maximum value of around 7.0 GPa. The accumulated internal energy in this deformation range is sufficient to rupture interatomic bonds at the crack tip. Moving to the second stage, within the deformation range of 4.8 – 5.2 %, the crack initiates propagation in the first grain. As the crack advances, a stacking fault is emitted from the crack tip, reaching the grain boundary ahead of the crack (Fig. 3, а). The dislocation is emitted into the second grain from the portion of the grain boundary reached by the stacking fault. The process of crack propagation results in an abrupt release of stress due to relaxation processes in the regions adjacent to the crack edges and the emission of defects from both the crack tip and the grain boundary. Upon reaching the grain boundary, the crack comes to a halt and undergoes blunting (Fig. 3, b, c). During the third stage, the crack remains within the grain boundary, and the sample stresses may undergo significant oscillations. These oscillations are attributed to the emission of various defects from both the grain boundary and the free surface of the second grain (Fig. 3, c). Notably, the emission of defects from the crack tip during this stage leads to local grain boundary migration in the vicinity of the crack, as clearly depicted in Fig. 3, b and c. During the third stage of crack evolution, it is noteworthy that stresses distribute unevenly across the sample as interfaces emit a substantial number of defects. The overall sample stress tends to decrease with increasing strain. However, if defects cease to be emitted from the crack tip, the stress in this specific region starts to rapidly grow, contrary to the decreasing trend observed in the entire sample. The onset of the fourth stage involves crack propagation into the second grain (Fig. 3, d), leading to an abrupt release of stress throughout the entire sample. Importantly, it should be emphasized that a boundary with a significant grain misorientation angle acts as a more effective barrier, restraining crack propagation into the adjacent grain and resulting in larger strain values.

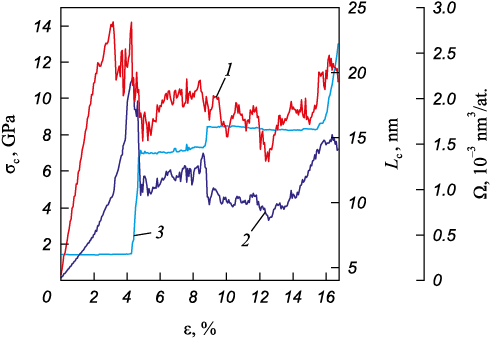
The simulation results demonstrate a clear correlation between changes in crack length and variations in stress and volume at the crack tip, as illustrated in Fig. 4. The distinct stages of crack opening are evident, with the crack propagating in discrete steps within the simulated bicrystal. It’s important to note that the stress release and subsequent increase during the first stage of crack evolution are associated with the nucleation and growth of a twin at the crack tip. The atomic volume experiences a rapid increase during the first stage, reaching an absolute maximum just before the crack opening (Fig. 4). The crack opening during the second stage results in a sharp drop in atomic volume and an abrupt stress release. In the third stage, a flat region on the curve is observed, reflecting the dependence of crack length on stress at a strain of approximately 9.0 %. This is associated with the crack opening along the boundary of a small twin formed near the grain boundary. Before the onset of the fourth stage, both atomic volume and stresses at the crack tip increase rapidly and then decrease as the crack opens into the second grain.

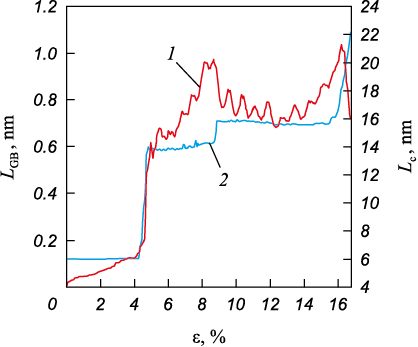
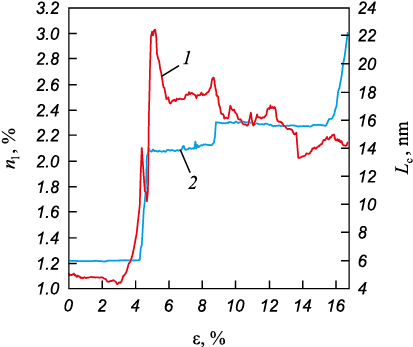
The simulation results further reveal that the interaction of the crack with the grain boundary initiates active migration of the latter (Fig. 5). This migration is most pronounced in a narrow strain range from 4.5 to 4.6 %, during which the distance between the crack and the grain boundary diminishes from several lattice constants to zero. In this case, the grain boundary undergoes substantial curvature, with the portion above the crack plane migrating towards the first grain, while the part below it shifts in the opposite direction (Fig. 1, b). As the strain approaches 8.5 %, when the crack remains within the grain boundary, migration slows down significantly. The abrupt cracking of the grain boundary caused by crack propagation at 8.5 % results in the migration of the grain boundary back towards its initial position. The grain boundary migration parameter exhibits oscillations, corresponding to the emission of structural defects from the grain boundary (Fig. 5). The growth rate of structural defects is highest when the crack tip approaches the grain boundary in the strain range of 4.0 – 4.5 % (Fig. 6). The grain boundary migration induced by the interaction with cracks is consistent with experimental findings obtained through transmission electron microscopy [22; 23].

Conclusions

The calculations have revealed that grain boundaries with a larger angle of misorientation in the iron bicrystal significantly retard crack propagation, leading to a prolonged presence of cracks in the intergranular region. In a bicrystal with a greater grain misorientation, the crack propagates a considerable distance along the grain boundary before transitioning into the second grain. It was observed that the initiation of seed crack propagation in the material is consistently preceded by an abrupt increase in atomic volume and stresses at the crack tip. The commencement of crack propagation invariably results in a sharp decrease in stress and atomic volume at the crack tip in the simulated bicrystals. Following the arrest of the crack by the grain boundary, both atomic volume and stress at the crack tip experience a subsequent increase. The interaction of the propagating crack with the grain boundary induces the migration of the grain boundary. Notably, grain boundaries exhibit the most active migration when the crack tip region is in contact with the grain boundary, particularly in the strain range where the crack tip comes in contact with the grain boundary.