Перейти к:
Взаимодействие трещины с границей зерен в бикристаллах железа
https://doi.org/10.17073/0368-0797-2023-6-718-724
Аннотация
Проведено молекулярно-динамическое моделирование эволюции затравочных трещин в бикристаллах железа с наклонными границами зерен при одноосном растяжении. Показано, что процесс эволюции затравочной трещины можно разбить на четыре этапа. На первом этапе в интервале упругих деформаций затравочная трещина неподвижна, а напряжения увеличиваются по линейному закону, достигая максимального значения ~7,0 ГПа. При этом атомный объем и напряжения в вершине трещины перед ее раскрытием растут существенно быстрее, чем в среднем по образцу. На втором этапе трещина начинает распространяться в объем зерна. Процесс распространения трещины приводит к скачкообразному сбросу напряжения за счет релаксационных процессов в областях, прилегающих к берегам трещины, и эмиссии дефектов из вершины трещины. Достигнув границы зерен, трещина останавливается и затупляется. На третьем этапе трещина остается в границе зерен, а напряжения образца испытывают существенные осцилляции, что вызвано эмиссией различных дефектов как из границы зерен, так и из других интерфейсов. Эмиссия дефектов из вершины трещины может вызвать локальную миграцию границы зерен, которая представляет собой формирование изгиба на изначально плоской поверхности границы зерен. Когда из вершины трещины перестают испускаться дефекты, то напряжение и атомный объем в этой области быстро увеличиваются. На четвертом этапе трещина начинается распространяться во второе зерно. Обнаружено, что граница с большим углом разориентации зерен является более эффективным барьером, сдерживающим распространение трещины. Показано, что инициированию распространения затравочной трещины в материале всегда предшествует скачкообразный рост атомного объема и напряжений в вершине трещины.
Ключевые слова
Для цитирования:
Крыжевич Д.С., Корчуганов А.В., Зольников К.П. Взаимодействие трещины с границей зерен в бикристаллах железа. Известия высших учебных заведений. Черная Металлургия. 2023;66(6):718-724. https://doi.org/10.17073/0368-0797-2023-6-718-724
For citation:
Kryzhevich D.S., Korchuganov A.V., Zol’nikov K.P. Interaction of cracks with grain boundaries in iron bicrystals. Izvestiya. Ferrous Metallurgy. 2023;66(6):718-724. https://doi.org/10.17073/0368-0797-2023-6-718-724
Введение
Исследованию поведения железа в процессе разрушения на микроскопическом уровне посвящено достаточно много работ. Вопросами исследований являлись установление влияний на развитие процессов разрушения в материале как особенностей внутренней структуры (дефектов, наночастиц, размеров зерен [1 – 4]), так и использование различных схем нагружения (граничные условия и скорости нагружения [5]), а также различные потенциалы межатомного взаимодействия [6]. Наиболее важную роль в зарождении и развитии разрушения в материале играют границы зерен (ГЗ). Характер взаимодействия между трещинами и границами зерен определяется рядом параметров, которые можно разделить на две группы [7]. К первой группе относят тип и интенсивность приложенной нагрузки, а также параметры трещины, в частности, ее длина и расстояние от трещины до границы зерен. Параметры трещины определяют концентрацию напряжений в ее вершине и выступают как движущая сила испускания и движения дислокаций. Во вторую группу входят параметры границы зерна, которые определяют уровень ее сопротивления распространению трещины. Для описания взаимодействия трещины с границей зерна наиболее часто используют две модели. В первой модели, разработанной и развитой в работах [8; 9], сопротивление границы зерна распространению трещины объясняется только ориентацией соседнего зерна, которая определяет положения плоскостей скольжения во втором зерне и эмиссию дислокаций в соответствующих системах скольжения. Во второй модели [10; 11] плоскость скольжения в соседнем зерне учитывается по-другому. В частности, при переходе границы зерен трещина должна изменить плоскость скольжения в сопряженном зерне. В этой модели два дополнительных параметра определяют величину сопротивления для роста трещин: поверхностная энергия границы зерен, характерная для разных типов границ зерен, и угол наклона границы зерна к поверхности.
Распространение трещины и разрушение представляют собой сложные явления, связанные с разрывом атомных связей и испусканием дислокаций из вершины трещины. Согласно линейной теории упругости поля напряжений в вершине трещины сингулярны [12]. Для устранения сингулярности и расчета точных полей напряжений можно использовать атомистическое моделирование процессов разрушения [13; 14]. В рамках молекулярно-динамического подхода были рассчитаны напряжения и локальная температура в вершине трещины и эмиссия из нее дислокаций в хрупком материале при режиме нагружения I. В работах [15; 16] было показано, что зарождение частичных дислокаций в вершине трещины при сдвиговом нагружении существенно зависит от температуры. Кроме того, режимы нагружения I, II, III или их комбинации в монокристалле железа оказывают заметное влияние на поведение трещины [13]. При этом характер пластичности в вершине трещины определяется кристаллографической ориентацией образца.
Для изучения эволюции разрушения в материале с зеренной структурой важное значение имеет выявление особенностей взаимодействия трещин с границами зерен. Экспериментальное изучение особенностей взаимодействия трещин в материале с заданным типом границ зерен достаточно сложно реализовать. В то же время взаимодействие трещин с любыми границами зерен можно детально исследовать в рамках метода молекулярной динамики. Несмотря на высокую эффективность этого метода в решении данного вопроса, соответствующих исследований для бикристаллов железа крайне мало. Следует отметить работу [17], в которой авторы исследовали сопротивление разрушению симметричных наклонных границ в бикристалле железа с затравочной трещиной. Было обнаружено, что время задержки трещины в границе зерна обратно пропорционально энергии границы зерна.
Целью настоящей работы является молекулярно-динамическое моделирование особенностей взаимодействия трещин, распространяющихся в хрупком режиме, с наклонными границами в бикристаллах железа при одноосном растяжении. Было исследовано влияние границ зерен на торможение и блокировку распространяющихся трещин, особенности миграции границ зерен при взаимодействии с трещиной, а также выявлены особенности изменения избыточного атомного объема и напряжения в вершине трещины в процессе ее эволюции и взаимодействия с границами зерен в бикристаллах железа.
Методы исследования
Моделируемые бикристаллы железа содержали около 950 000 атомов и имели форму параллелепипедов с размерами ребер 27×40×10 нм (рис. 1). Ребра правых зерен на рисунке всегда были ориентированы вдоль направлений X [\(1\bar 20\)], Y [210], Z [001]. Зерно в левой части бикристалла было повернуто вокруг оси Z на 10 или 20°. Исходная температура в моделируемых образцах составляла 10 К. Вдоль оси X задавались свободные поверхности, вдоль оси Z были использованы периодические граничные условия. Три поверхностные атомные плоскости с нормалью вдоль оси Y задавались как недеформируемые захваты, которые смещались в противоположных направлениях вдоль оси Y со скоростью 2,5 м/с каждый, имитируя одноосное растяжение образца.
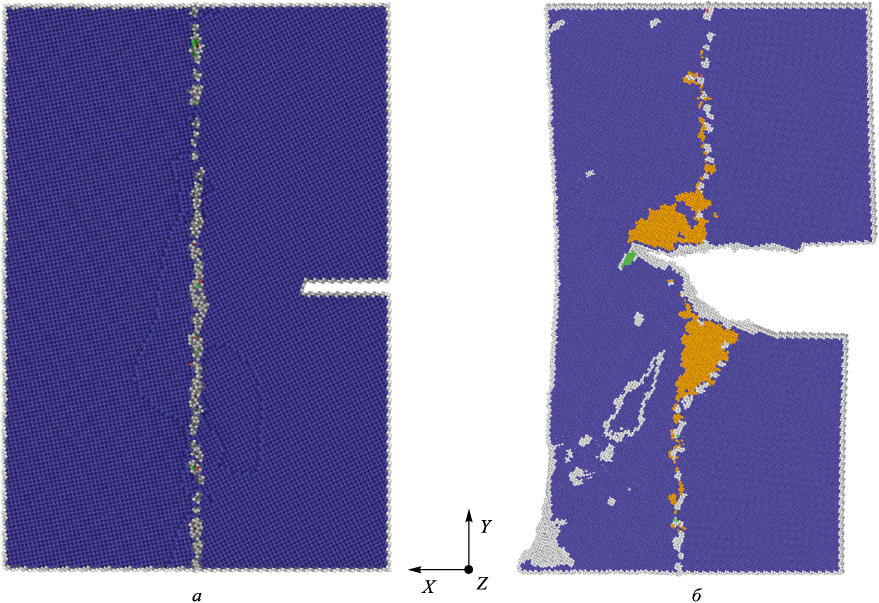
Рис. 1. Исходная структура бикристалла железа с разориентацией зерен 10° (a) |
Межатомное взаимодействие в железе описывалось многочастичным потенциалом, разработанным в рамках приближения Финниса–Синклера метода погруженного атома [18]. Распределение скоростей атомов в исходном образце соответствовало распределению Максвелла, а начальное направление скоростей атомов задавалось с помощью генератора случайных чисел. Шаг интегрирования задавался равным 1 фс. Атомные объемы рассчитывались на основе построения многогранников Вороного. Для идентификации локальных структурных изменений в нагружаемом образце использовался алгоритм анализа по общим соседям для каждого атома [19]. Угол отклонения атомной решетки относительно оси [100] определялся с помощью алгоритма Polyhedral Template Matching (PTM) [20]. Для визуализации структуры моделируемых кристаллитов использовался пакет OVITO [21].
Для расчета избыточного объема в вершине трещины строился цилиндр радиусом R = 1,2 нм. За вершину трещины принимался один из атомов на ее поверхности с максимальной координатой X. Ось цилиндра совпадала с направлением оси Z. Для расчета атомного объема в вершине трещины цилиндр смещался вдоль осей X и Y на расстояние от –R до +R относительно атома в вершине трещины c шагом 0,1R. Проводился расчет суммарного объема атомов внутри цилиндра как сумма объемов ячеек Вороного и затем выбиралось его максимальное значение. Избыточный объем атома определялся как разница между объемом ячейки Вороного и равновесным атомным объемом для данной температуры. Избыточный объем в вершине трещины рассчитывался как среднее избыточных объемов атомов, попавших в цилиндр с максимальным объемом.
Для расчета миграции границы зерен в окрестности каждого атома на основе использования алгоритма PTM определялся угол отклонения локальной решетки от оси X. Полагалось, что атомы, отклонение которых от выбранной оси превышало половину величины угла разориентации зерен, принадлежат второму зерну, а остальные атомы составляют первое зерно. В процессе нагружения выявлялись атомы, которые перешли из состава одного зерна в другое. Объем образца (dV), через который мигрировала ГЗ относительно своего исходного положения, рассчитывался как суммарный атомный объем этих атомов (рис. 1, б). Параметр миграции ГЗ в направлении оси X определялся по формуле: LГЗ = dV/SX (где SX – площадь сечения деформированного образца плоскостью, перпендикулярной оси X).
Результаты моделирования поведения трещин
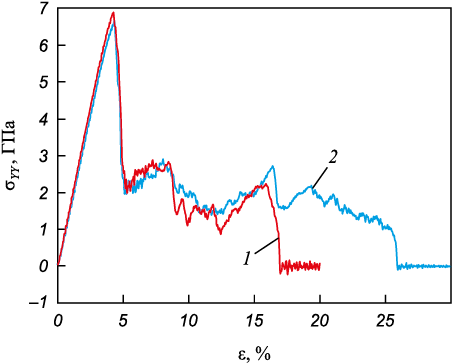
Результаты расчетов зависимости напряжений от деформации для бикристаллов с разориентациями зерен 10 и 20° приведены на рис. 2. Хорошо видно, что разрушение образца с разориентацией зерен 20° наступает при значительно большей деформации: примерно 26 %. В целом, поведение кривых для этих двух границ зерен качественно совпадает. Поведение кривых деформации (рис. 2) показывает, что процесс распространения трещин в бикристаллах можно разбить на четыре этапа. Детальный анализ развития разрушения был проведен применительно к образцу с разориентацией зерен 10°. На первом этапе в интервале упругих деформаций 0 – 4,8 % затравочная трещина неподвижна, а напряжения увеличиваются по линейному закону, достигая максимума (~7,0 ГПа). При этой деформации запасенной внутренней энергии становится достаточно для разрыва межатомых связей в вершине трещины. На втором этапе в интервале деформирования 4,8 – 5,2 % трещина начинает распространяться в первом зерне. В процессе распространения трещины из ее вершины испускается дефект упаковки, который достигает границы зерен раньше, чем трещина (рис. 3, а). Из участка границы зерна, которого достиг дефект упаковки, испускается дислокация во второе зерно. Процесс распространения трещины приводит к скачкообразному сбросу напряжения за счет релаксационных процессов в областях, прилегающих к берегам трещины, и эмиссии дефектов из вершины трещины и границы зерен. Достигнув границы зерен, трещина останавливается и затупляется (рис. 3, б, в). На третьем этапе трещина покоится в границе зерен, а напряжения образца могут испытывать существенные осцилляции, которые связаны с эмиссией различных дефектов как из границы зерен, так и от свободной поверхности второго зерна (рис. 3, в). Хорошо видно (рис. 3, б, в), что эмиссия дефектов из вершины трещины на третьем этапе приводит к локальной миграции границы зерен вблизи трещины. Следует отметить, что на третьем этапе эволюции трещин распределение напряжений существенно неоднородно по образцу из-за эмиссии интерфейсами большого числа дефектов. Напряжение всего образца с увеличением деформации имеет тенденцию к уменьшению. Однако, если из вершины трещины перестают испускаться дефекты, то напряжение в этой области начинает быстро увеличиваться, а не уменьшаться, как в целом по образцу. Четвертый этап начинается с распространения трещины во второе зерно (рис. 3, г), что приводит к скачкообразному падению напряжения всего образца. Следует отметить, что граница с большим углом разориентации зерен является более эффективным барьером, сдерживающим распространение трещины в соседнее зерно до больших величин деформации.
Рис. 2. Зависимость напряжений от деформации
Рис. 3. Структура образца с разориентацией зерен 10° при деформациях 4,57 (a), |
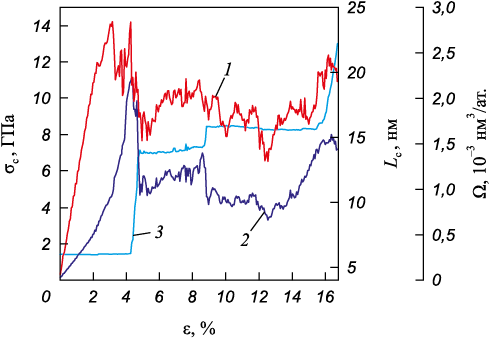
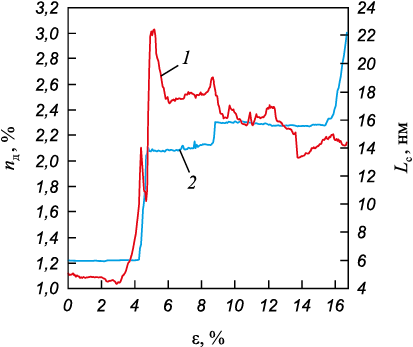
Результаты моделирования показали, что особенности изменения длины трещины коррелируют с изменениями напряжения и объема в вершине трещины (рис. 4). Хорошо видны вышеописанные этапы раскрытия трещины, распространение которой в моделируемом бикристалле носит скачкообразный характер. Отметим, что падение и последующий рост напряжения на первом этапе эволюции трещины связан с зарождением и ростом двойника в вершине трещины. Атомный объем на первом этапе достаточно быстро нарастает и достигает абсолютного максимума перед началом раскрытия трещины (рис. 4). Раскрытие трещины на втором этапе ее эволюции ведет к скачкообразному падению не только напряжения, но и атомного объема. На третьем этапе хорошо видна ступенька на кривой зависимости длины трещины от напряжения при деформации примерно 9,0 %. Она связана с раскрытием трещины вдоль границы небольшого двойника, сформированного вблизи границы зерен. Перед началом четвертого этапа атомный объем и напряжения в вершине трещины достаточно быстро растут, а с раскрытием трещины во второе зерно падают.
Рис. 4. Зависимости напряжения (1), атомного объема (2) |
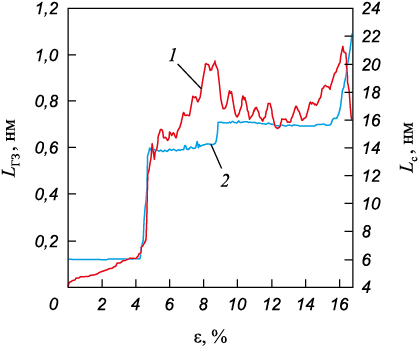
Результаты моделирования показывают, что взаимодействие трещины с границей зерен инициирует активную миграцию последней (рис. 5). Наиболее активная миграция происходит в достаточно узком интервале деформаций от 4,5 до 4,6 %, на котором расстояние между трещиной и границей зерна сокращается с нескольких параметров решетки до нуля. При этом граница зерен существенно искривляется. Граница зерен, расположенная выше плоскости трещины, мигрирует в сторону первого зерна, а часть, расположенная ниже, смещается в противоположном направлении (рис. 1, б). В интервале деформаций до 8,5 %, когда трещина покоится в границе зерен, миграция существенно замедляется. Процесс скачкообразного растрескивания границы зерен в результате распространения трещины при 8,5 % приводит к миграции границы зерен в направлении ее исходного положения. Параметр миграции границы зерен испытывает осцилляции, связанные с эмиссией дефектов структуры из границы зерен (рис. 5). При этом наиболее высокая скорость роста дефектов структуры наблюдается в процессе сближения вершины трещины с границей зерен на интервале деформаций 4,0 – 4,5 % (рис. 6). Миграция границ зерен, инициированная взаимодействием с трещинами, подтверждается экспериментальными данными, полученными посредством просвечивающей электронной микроскопии [22; 23].
Рис. 5. Зависимость параметра миграции ГЗ (1) и длины трещины (2) от деформации
Рис. 6. Зависимость доли атомов, принадлежащих различным |
Выводы
Проведенные расчеты показали, что границы с большим углом разориентации зерен в бикристалле железа существенно эффективнее тормозят движение трещин, что проявляется в более длительной задержке трещин в межзеренной области. Для бикристалла с большей разориентацией зерен трещина, прежде чем перейти во второе зерно, распространяется на некоторое расстояние вдоль по границе зерен. Обнаружено, что инициированию распространения затравочной трещины в материале всегда предшествует скачкообразный рост атомного объема и напряжений в вершине трещины. Начало распространения трещины всегда вызывает скачкообразное уменьшение напряжения и атомного объема в вершине трещины в моделируемых бикристаллах. После остановки трещины границей зерен атомный объем и напряжение в вершине вновь возрастают. Выявлено, что взаимодействие распространяющейся трещины с границей зерен приводит к миграции последней. При этом наиболее активная миграция границы зерен происходит в интервале деформации, когда область вершины трещины контактирует с границей зерен.
Список литературы
1. Uhnáková A., Machová A., Hora P., Červená O. Growth of a brittle crack (001) in 3D bcc iron crystal with a Cu nano-particle. Computational Materials Science. 2014;83:229–234. http://dx.doi.org/10.1016/j.commatsci.2013.10.037
2. Farkas D. Atomistic simulations of metallic microstructures. Current Opinion in Solid State and Materials Science. 2013;17(6):284–297. https://doi.org/10.1016/J.COSSMS.2013.11.002
3. Liu T., Groh S. Atomistic modeling of the crack–void interaction in α-Fe. Materials Science and Engineering: A. 2014;609:255–265. https://doi.org/10.1016/J.MSEA.2014.05.005
4. Latapie A., Farkas D. Molecular dynamics investigation of the fracture behavior of nanocrystalline α-Fe. Physical Review B. 2004;69:134110. https://doi.org/10.1103/PhysRevB.69.134110
5. Tanaka M., Tarleton E., Roberts S.G. The brittle–ductile transition in single-crystal iron. Acta Materialia. 2008;56(18):5123–5129. https://doi.org/10.1016/J.ACTAMAT.2008.06.025
6. Gordon P.A., Neeraj T., Luton M.J. Atomistic simulation of dislocation nucleation barriers from cracktips in α-Fe. Modelling and Simulation in Materials Science and Engineering. 2008;16:045006. https://doi.org/10.1088/0965-0393/16/4/045006
7. Schaef W., Marx M., Vehoff H., Heckl A., Randelzhofer P. A 3-D view on the mechanisms of short fatigue cracks interacting with grain boundaries. Acta Materialia. 2011;59(5):1849–1861. https://doi.org/10.1016/j.actamat.2010.11.051
8. Tanaka K., Akiniwa Y., Nakai Y., Wei R.P. Modelling of small fatigue crack growth interacting with grain boundary. Engineering Fracture Mechanics. 1986;24(6):803–819. https://doi.org/10.1016/0013-7944(86)90266-3
9. Navarro A., de los Rios E.R. Short and long fatigue crack growth: A unified model. Philosophical Magazine A. 1988;57(1):15–36. https://doi.org/10.1080/01418618808204496
10. Zhai T., Wilkinson A.J., Martin J.W. A crystallographic mechanism for fatigue crack propagation through grain boundaries. Acta Materialia. 2000;48(20):4917–4927. https://doi.org/10.1016/S1359-6454(00)00214-7
11. Zhai T., Jiang X.P., Li J.X., Garratt M.D., Bray G.H. The grain boundary geometry for optimum resistance to growth of short fatigue cracks in high strength Al-alloys. International Journal of Fatigue. 2005;27(10-12):1202–1209. https://doi.org/10.1016/J.IJFATIGUE.2005.06.021
12. Lemaitre J., Chaboche J.-L. Mechanics of Solid Materials. Cambridge University Press; 1990:584. https://doi.org/10.1017/CBO9781139167970
13. Ringdalen Vatne I., Stukowski A., Thaulow C., Østby E., Marian J. Three-dimensional crack initiation mechanisms in bcc-Fe under loading modes I, II and III. Materials Science and Engineering: A. 2013;560:306–314. https://doi.org/10.1016/J.MSEA.2012.09.071
14. Konovalenko I.S., Kryzhevich D.S., Zol’nikov K.P., Psakhie S.G. Atomic mechanisms of local structural rearrangements in strained crystalline titanium grain. Technical Physics Letters. 2011;37(10):946–948. https://doi.org/10.1134/S1063785011100233
15. Zhang Y.W., Wang T.C., Tang Q.H. Simulation of nucleation and emission of dislocations by molecular‐dynamics method. Journal of Applied Physics. 1995;77(6):2393–2399. https://doi.org/10.1063/1.358764
16. Zhang Y.W., Wang T.C., Tang Q.H. The effect of thermal activation on dislocation processes at an atomistic crack tip. Journal of Physics D: Applied Physics. 1995;28:748–754. https://doi.org/10.1088/0022-3727/28/4/018
17. Pezeshki S.S., Silani M., Talaei M.S., Ziaei-Rad S. An atomistic perspective into the fracture behaviour of Fe-bicrystal. Molecular Simulation. 2020;46(13):966–974. https://doi.org/10.1080/08927022.2020.1795165
18. Mendelev M.I., Han S., Son W.-j., Ackland G.J., Srolovitz D.J. Simulation of the interaction between Fe impurities and point defects in V. Physical Review B. 2007;76:214105. https://doi.org/10.1103/PhysRevB.76.214105
19. Honeycutt D.J., Andersen H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. The Journal of Physics Chemistry. 1987; 91(19):4950–4963. https://doi.org/10.1021/j100303a014
20. Larsen P.M., Schmidt S., Schiøtz J. Robust structural identification via polyhedral template matching. Modelling and Simulation in Materials Science and Engineering. 2016;24(5):055007. https://doi.org/10.1088/0965-0393/24/5/055007
21. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modelling and Simulation in Materials Science and Engineering. 2010;18(1):015012. https://doi.org/10.1088/0965-0393/18/1/015012
22. Legros M., Gianola D.S., Hemker K.J. In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films. Acta Materialia. 2008;56(14):3380–3393. https://doi.org/10.1016/j.actamat.2008.03.032
23. Rupert T.J., Gianola D.S., Gan Y., Hemker K.J. Experimental observations of stress-driven grain boundary migration. Science. 2009;326(5960):1686–1690. https://doi.org/10.1126/science.1178226
Об авторах
Д. С. КрыжевичРоссия
Дмитрий Сергеевич Крыжевич, к.ф.-м.н., научный сотрудник лаборатории компьютерного конструирования материалов
Россия, 634055, Томск, пр. Академический, 2/4
А. В. Корчуганов
Россия
Александр Вячеславович Корчуганов, к.ф.-м.н., научный сотрудник лаборатории компьютерного конструирования материалов
Россия, 634055, Томск, пр. Академический, 2/4
К. П. Зольников
Россия
Константин Петрович Зольников, д.ф.-м.н., главный научный сотрудник лаборатории компьютерного конструирования материалов
Россия, 634055, Томск, пр. Академический, 2/4
Рецензия
Для цитирования:
Крыжевич Д.С., Корчуганов А.В., Зольников К.П. Взаимодействие трещины с границей зерен в бикристаллах железа. Известия высших учебных заведений. Черная Металлургия. 2023;66(6):718-724. https://doi.org/10.17073/0368-0797-2023-6-718-724
For citation:
Kryzhevich D.S., Korchuganov A.V., Zol’nikov K.P. Interaction of cracks with grain boundaries in iron bicrystals. Izvestiya. Ferrous Metallurgy. 2023;66(6):718-724. https://doi.org/10.17073/0368-0797-2023-6-718-724
JATS XML