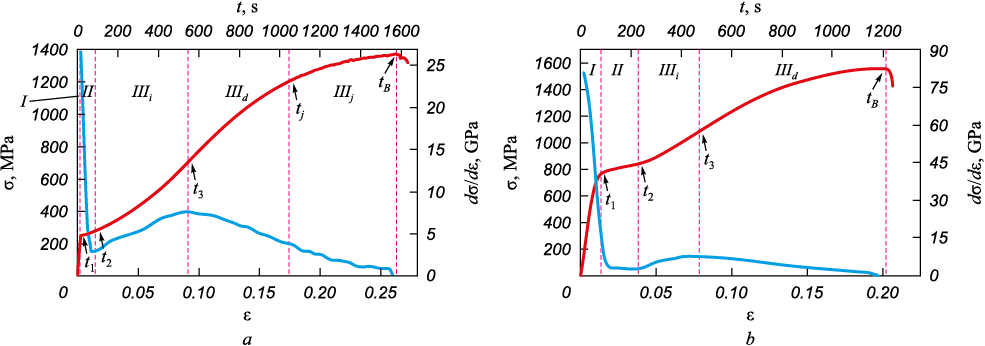Lüders and Portevin–Le Chatelier processes in austenitic-martensitic TRIP steel

Introduction

The utilization of the autowave concept to characterize Lüders deformation in low-carbon steel has proven to be productive [1]. This conceptual framework enabled the establishment of the nonlinear relationship between the speed of Lüders fronts and the deformation rate, shedding light on the underlying reasons for this nonlinearity. It is recognized that, at the microscopic level in low-carbon steel, the emergence of Chernov-Lüders bands (ChLB) is attributed to two competing processes: the thermally activated movement of dislocations, where the primary barriers are “forest” dislocations, and their additional hindrance due to the deposition of impurity atoms on mobile dislocations (effect of dynamic strain aging) [2 – 4]. Nevertheless, certain materials, such as shape memory alloys and certain steels with a metastable phase structure, exhibit ChLB formation at the microlevel not linked to dislocation processes but rather to deformation-induced phase transformation [5 – 8]. This raises the question of how applicable the autowave concept of plastic flow is in such cases.

In response to the demands of technological practice, the advancement of insights into the mechanisms governing thermoelastic phase transformations has contributed to the development of TRIP-steels (transformation induced plasticity), characterized by high strength coupled with significant plasticity. This steel class encompasses metastable austenitic–ferritic [8] and austenitic–martensitic steels [9]. The attainment of the TRIP effect is contingent upon the nature of changes in metastable austenite volume fraction during mechanical processing. This process is influenced by various parameters, including the crystal lattice orientation, temperature, deformation rate, degree of hardening, and the heterogeneity of alloying element distribution [10 – 13]. For example, the authors of [12] demonstrated that the disparate stability of austenite in austenitic–ferritic TRIP steels stems from the nonuniform distribution of manganese. Similarly [9], established that the stability of austenite in austenitic–martensitic TRIP steel varies based on the reduction amount during “warm” rolling. When the degree of hardening of the austenite phase is substantial, the transformation occurs at high stresses and is fully completed at the yield point. If the hardening is not significant and the yield strength is low, only a small portion of the austenite transforms into the martensite phase at the yield site. The transition in the remaining austenite grains occurs in subsequent stages of the loading curve through the mechanism of formation and propagation of Portevin–Le Chatelier (PLCh) bands. It was noted in [14] that the fronts of the Chernoff–Lüders bands (ChLB) and the fronts of the PLCh bands represent distinct autowave modes. As the processes of shape change in austenitic–martensitic TRIP steels unfold through the thermoelastic transformation of non-magnetic austenite into a magnetic martensitic phase, the objective of this study is to examine the kinetics of localized plastic deformation fronts concurrently with the characterization of martensite accumulation patterns based on the material’s magnetization magnitude.

Materials and methods

The investigations were conducted on samples of VNS9-Sh (23Kh15N5AM3-Sh) TRIP steel. 1 mm thick plates as delivered underwent austenitization (hardening) with a 1 h exposure at a temperature of T = 1400 K, followed by cooling in water. Subsequently, multi-pass warm rolling was performed at a temperature of 620 K with a 40 % reduction. Following austenitization, the steel exhibited a low yield strength (σ_0.2 = 250 MPa) and high plasticity (δ = 27 %). Hardening during rolling resulted in an almost threefold increase in yield strength (σ_0.2 = 735 MPa), accompanied by a reduction in plasticity to 20 %. The austenitized state is denoted as 1, and the rolled state as 2. The chemical composition of VNS9-Sh steel is as follows (by weight): 0.25 % C; 14.5 – 16.0 % Cr; 4.8 – 5.8 % Ni; 2.7 – 3.2 % Mo; 0.03 – 0.07 % N; ≤1 % Mn; ≤0.6 % Si; ≤0.01 % S; ≤0.015 % P.

Using the electric spark method, samples of the “double blade” type with working part dimensions of 40×6 mm were cut from the workpieces. The samples underwent uniaxial tension testing at room temperature using a Walter + Bai AG universal testing machine, LFM 125 series. The moving speed of the movable gripper (V_mach) was set at 0.4 mm/min, ensuring a deformation rate of 1.67·10\(^–\)⁴ s\(^–\)¹.

Throughout the stretching process, digital images of the deformed sample were sequentially recorded, following a procedure similar to the one outlined in [1]. The recorded series of images served for the identification of areas with localized deformation, and their kinetics were analyzed using the traditional method of digital image correlation (DIC) [15]. Utilizing the obtained data arrays, chronograms were constructed [1; 16], enabling the detection of regions of origin, movement, and annihilation of localized deformation fronts.

Simultaneously, changes in the martensite content in the samples were determined in situ by measuring the magnetization of the material using an MVP-2M multifunctional eddy current device. This magnetic measurement method allows for the quantification of the volume fraction of the magnetic phase without the necessity of interrupting mechanical tests. The magnetic measurement sensor remained in contact with the working part of the sample throughout the entire loading duration, with a sensor probe diameter of 2 mm.

Results

Fig. 1 depicts the strain curves σ(ε) and the corresponding variations in the strain hardening coefficient θ(ε) = dσ/dε(ε) for samples in states 1 and 2. A comprehensive analysis of these dependencies facilitate identification of five distinct areas: I, II, III_i, III_d, III_j . Section I (0 – t₁) corresponds to elastic loading and microplasticity (not shown in the θ(ε) dependence for state 1). Section II (t₁ – t₂) includes a weakly defined tooth and an imperfect yield plateau (referred to as a pseudo plateau in the terminology of [16]). Following section II, the nonlinear stage III begins with a positive hardening coefficient. In section III_i (t₂ – t₃) the hardening coefficient increases from zero to its maximum value. Section III_d (t₃ – t_δ) is characterized by a decline in the hardening coefficient from its maximum value to zero, akin to the traditional parabolic strain curve described by the Hollomon–Ludwik equation σ = σ₀ + Kε\(^{n}\) (where K is the strain hardening coefficient and n is the strain hardening index, with n < 1). In the austenitized state 1, stress surges are observed against the backdrop of this curve (section III_j, t_j – t_δ). The Table provides the values of time and deformation corresponding to the boundaries of the stages and sections.

The magnetic measurements conducted during the tensile tests of the sample enabled the characterization of the process of martensitic phase accumulation and, consequently, a reduction in the volume fraction of metastable austenite. Throughout deformation, the content of the austenite phase in steel decreased from 93 % to approximately 30 % in state 1, and from 80 % to approximately 40 % in state 2 (Fig. 2).

As established in [17], the deformation of TRIP steels develops locally through the formation and movement of deformation fronts. In the present work, it has been demonstrated that the kinetics of deformation fronts align not only with the stages of the hardening curve but also with changes in the phase composition.

Fig. 3 shows the initial section of the chronograms depicting the movement of deformation fronts in TRIP steel in states 1 and 2. The chronograms are constrained to 810 s (state 1) and 1150 s (state 2) due to the significantly higher amplitudes of deformation in the destruction zone compared to the pseudo plateau. This sharp inhomogeneity in contrast complicates the perception of fronts in the early stages of deformation. It is evident that in all sections, except for section I, localized deformation fronts are in motion. During the pseudo plateau stage, ChLBs form in both states, denoted as A, B, C and A, B, C, D, Е for states 1 and 2, respectively.

The chronogram in Fig. 3, a (state 1), illustrates that the Lüders band A appeared on the yield tooth at time t₁. Subsequently, bands B and C were formed, and their fronts (boundaries) moved in pairs towards each other, culminating in annihilation at time t₂. At this juncture, the entire working area of the sample has transitioned into a plastically deformed state. The regions of annihilation of Lüders fronts play a pivotal role in the subsequent stages.

In all sections of nonlinear stage III, there is also the movement of localized deformation fronts (Fig. 3, a). However, initially, they originate and spread within the boundaries set by the annihilation zones of the Lüders fronts. The movement of deformation fronts during stage III is such that, overall, they traverse the entire sample multiple times. As section III_j commences, the regions of annihilation of Lüders fronts cease to serve as boundaries for the movement of deformation fronts during stage III.

In state 2 (Fig. 3, b) in the pseudo plateau area, the scenario is analogous to that described for state 1, albeit with a higher generation of Chernov–Lüders bands (ChLB). The regions of annihilation of Lüders fronts continue to act as constraints on the movement of deformation fronts during stage III. However, in this case, such fronts move only up to approximately 700 s. Following this period, macro-level deformation localization is absent until the formation of a fracture neck at t_δ = 1214 s.

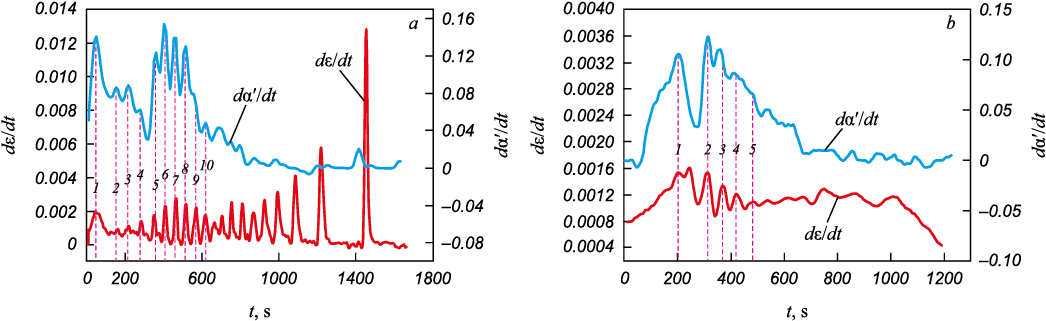
In a previous study [17], it was hypothesized that the observed fronts of localized deformation are attributed to the progression of the γ → α′ phase transformation. If this assumption holds true, the accumulation of the martensite phase should align with the kinetics of deformation fronts. In Fig. 3, horizontal blue lines denote the coordinates where the magnetic measurement sensor is positioned on the working part of the sample; the numbers indicate the instances of the passage of localized deformation fronts through these coordinates. As the deformation front traverses the specified point, the rate of strain accumulation dε/dt sharply increases, as evident in Fig. 4. Time instant 1 (state 1) corresponds (Fig. 4, a) to the passage of front A of the Lüders band through the magnetic sensor probe, while the subsequent instances (2 – 10) denote the passage of localized deformation fronts during stage III.

In Fig. 4, a, the dependence of the rate of martensite phase accumulation on time in state 1 is also depicted. It is evident that the passage of front A of the Lüders band at time 1 corresponds to the maximum rate of formation of the magnetic phase of α′ martensite. It is estimated that up to 10 % of the magnetic phase is formed on the pseudo plateau. The remaining transformation γ → α′ primarily occurs in the nonlinear section III_i under conditions of increasing hardening rate. Here, too, the maximum rate of martensite formation aligns with times 2 – 10, coinciding with the passage of deformation fronts through the probe. The highest transformation rates are observed at times of passage of fronts 5 – 8. In total, approximately 50 % of the martensite phase is formed in section III_i. As section III_d begins (t₃ = 545 s), the transformation rate sharply decreases, and the correspondence between the time of passage of deformation fronts and the maximum rates of γ → α′ transformation is disrupted. By the start of section III_j (t_j = 1050 s), the rate of γ → α′ transformation nearly becomes zero (Fig. 4, a), and the content of α′ martensite reaches 69 %, remaining almost unchanged (Fig. 2). Simultaneously, the deformation fronts continue to propagate, and their amplitudes even increase (Fig. 3, a and 4, a).

In state 2 (Fig. 4, b) the situation is generally similar. However, pseudo plateau (section II) produces markedly more martensite (≈15 %). Additionally, even though the duration of section III_i is significantly shorter in state 2, almost 40 % of martensite has been formed within this section. Here as well, the maximum rate of α′ phase formation corresponds to the passage of deformation fronts through the probe of the magnetic sensor. As the section III_d commences, similar to state 1, the transformation rate sharply decreases to zero. The synchronicity between the maximum velocities γ → α′ and the times of passage of deformation fronts is disrupted, and the amount of martensite, having reached 60 %, remains unchanged further (Fig. 4, b and Fig. 2). It is worth noting that in state 2, in section III_d, there is no movement of deformation fronts, no stress drops, and the σ(ε) diagram remains smooth until failure (Fig. 1, b and Fig. 3, b).

Discussion

The thermoelastic martensitic transformation in the TRIP steel under investigation can potentially occur throughout the entire deformation process, spanning from the yield point to fracture. However, the sequence of macroscopic manifestations and the completeness of this process are contingent on various external factors. For instance, as demonstrated by the authors of [10], the γ → α′ transformation in VNS9-Sh steel never reaches completion. As the deformation rate and test temperature increase, a greater quantity of “stable” austenite, as per the authors’ terminology, remains. At room temperature and a stretching rate of approximately 10\(^–\)⁴ s\(^–\)¹, about 70 % of austenite is retained, aligning with the findings obtained in this study.

It is commonly asserted that the thermoelastic transformation γ → α′ in TRIP steels is primarily facilitated through the formation of ChLB [7; 10], and then continues in the form of the Portevin–Le Chatelier effect [7; 10; 17]. The findings of this study generally align with this concept. However, in a previous investigation [18], it was demonstrated that at a high level of hardening of metastable austenite, the transformation can be entirely completed by the formation of ChLB at the yield site, and further deformation occurs without the involvement of a phase transformation.

Building upon the results of this study (VNS9-Sh in state 1, low yield strength), it was established that after Lüders deformation, the phase transformation indeed continues through the formation and propagation of PLCh bands, but only while the strain hardening rate increases. Upon transitioning to the section of the deformation curve with a decreasing hardening rate, the transformation diminishes and comes to a complete halt in the region of abrupt deformation. The observed discontinuous flow thereafter is not associated with a phase transformation and appears to be explained, similar to stable austenitic steels, by twinning [19]. When the steel under study was in state 2 (high yield stress), phase transformation also occurred through the formation of both ChLB and PLCh bands. However, the latter were observed only in the section of the loading diagram with an increasing hardening coefficient. Subsequently, the deformation developed monotonically.

As mentioned in [18; 20], the kinetics of deformation fronts in materials undergoing deformation-induced phase transformation can be explained using autowave theory [21; 22]. In this conceptual framework, ChLB fronts are considered autowaves of switching localized plasticity. Switching autowaves traverse the loaded object once, transitioning it from an elastically stressed to a plastically deformed state. These autowaves are formed in media with bistable active elements, that can operate just once.

A deformable body can serve as a medium with excitable active elements that, unlike bistable ones, can return to a state of excitation under external influence and relax again after a refractory period. In this scenario, localized plasticity excitation autowaves are formed, which can pass through the deformable object multiple times. These autowaves represent the fronts of the PLCh bands.

Within the framework of autowave theory, the obtained results can be interpreted as follows. Multiple ChLBs are formed on the pseudo plateau, and the moving boundaries of these bands can be considered as switching autowaves. These autowaves partially transition the material from the metastable austenitic state to the stable martensitic state. In the regions of autowave generation and annihilation, the material undergoes a radical change in state, leading to the division of the sample into relatively isolated sections. A notable characteristic of the thermoelastic phase transformation is its self-blocking nature due to internal stresses. However, with a subsequent increase in external stresses, the transformation can resume. Therefore, the regions of origin and annihilation of primary autowaves, where the material’s state is significantly distorted, act as sources for new phase transformation fronts, referred to as secondary autowaves of excitation. These secondary waves propagate within the formed isolated areas without crossing their boundaries. This process repeats multiple times as long as there is austenite capable of transformation. As indicated by magnetic measurements, the γ → α′ transformation halts when section III_d begins. Simultaneously, the boundaries of the isolated areas cease to play a role, allowing deformation fronts to freely traverse the entire sample pattern. While these fronts are also autowaves of excitation, their physical nature is different. They do not represent a relay phase transformation but rather shear processes, likely of a twin nature.

Conclusions

Plastic deformation of VNS9-Sh TRIP steel can occur locally throughout the entire strain curve, spanning from the yield point to fracture. Initially, the process involves the generation and propagation of localized plasticity switching autowaves, induced by the deformation-induced transformation of metastable austenite into α′-martensite. The process persists via propagation of localized plasticity switching autowaves within boundaries determined by primary switching autowaves. Following the depletion of transformable austenite, steel deformation takes place through dislocation or twin mechanisms.