Scroll to:
Increasing the fatigue strength of high-strength steel grades
https://doi.org/10.17073/0368-0797-2023-5-522-528
Abstract
The paper considers the issue of increasing the fatigue strength of high-strength steel grades. Based on the results of experimental measurements of the fatigue strength limit (σ–1) of spring steel grades, we analyzed the effect of tensile strength, ratio of the yield strength during shear and the fatigue strength limit. The absence of statistical relationship between fatigue strength limit and tensile strength (σ–1 ≠ f (σu)) was established. The ratio τt / σ–1 is the stress concentration coefficient (SCC), which is closely related to the tensile strength of steel. From the theoretical analysis, it follows that in the presence of the same morphological type and size of non-metallic inclusions (NMI) in steel, relationship of SCC with the strength properties of steel is functional. Spread of its actual values is associated with the presence of various morphological types and sizes of NMI in the metal. Each morphological type of NMI is characterized by corresponding physical and mechanical properties (modulus of elasticity, tensile strength and various SCC). SCC increases both with an increase in the strength of steel and with an increase in diameter (thickness) of NMI. It was established that the intensity (rate) of the increase in SCC depends on the size and elastic modulus ЕMNI of NMI (ratio of mass fractions of SiO2 and Al2O3 oxides in NMI). The average intensity of the change in SCC obtained by processing experimental data corresponds to similar indicators for NMI: 13 % SiO2 ; 87 % Al2O3 (4.0 μm thick); 20 % SiO2 , 80 % Al2O3 (5.0 μm thick); 25 % SiO2 ; 75 % Al2O3 (7.0 μm thick). According to the obtained connections, dimensions of NMI and their morphology are approximately indicated, which make it possible to increase the fatigue properties of spring steels grades in the tensile strength range from 1200 to 2000 MPa. To increase the fatigue life of steel (especially in high-strength condition), it is recommended to use the technology of aluminum-free metal deoxidation during smelting. At the same time, a favorable morphology of NMI with SCC less than 1.0 is provided. Formation of a fine-grained structure of steel after heat treatment is obtained in the absence of aluminum during deoxidation with small additives of vanadium, niobium or titanium.
Keywords
For citations:
Pavlov V.V., Temlyantsev M.V., Bukhmirov V.V. Increasing the fatigue strength of high-strength steel grades. Izvestiya. Ferrous Metallurgy. 2023;66(5):522-528. https://doi.org/10.17073/0368-0797-2023-5-522-528
Introduction
The fatigue strength stands as a critical parameter for metals and alloys, profoundly influencing their potential applications as structural materials across diverse industrial sectors [1; 2]. Among the spectrum of structural metal alloys, steels persist as the most prevalent choice for fabricating a wide range of metal products and structures, especially those subjected to heavy-duty operations. In instances such as rail and spring steels enduring dynamic and fluctuating loads [3; 4], the fatigue strength assumes paramount importance, directly dictating the operational lifespan of metal products [5; 6]. It’s noteworthy that fatigue strength isn’t solely contingent upon the chemical and phase compositions of steel or its structural configuration [7; 8], but also on factors such as dimensions, non-metallic inclusion morphology, and operational conditions of the metal products [9; 10]. Notably, strain hardening emerges as a viable method to influence fatigue strength positively [11 – 13]. Consequently, enhancing steel’s fatigue strength remains a pressing research imperative in contemporary materials science endeavors [14].
Materials and methods
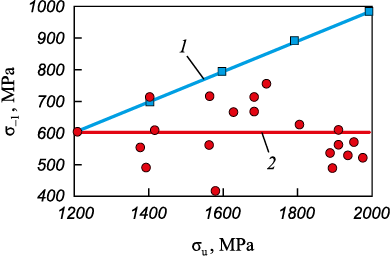
The known relationship σ–1 = 0.5σu (where σ–1 and σu is fatigue strength and σu is tensile strength) is valid for steel with the tensile strength not exceeding 900 MPa [15; 16]. However, as the strength surpasses this threshold, the actual values of fatigue strength significantly deviate from the calculated ones [17; 18] (Fig. 1). This study focuses on exploring the correlation between fatigue strength and tensile strength in spring steel using regression analysis methods. The specific values of tensile strength (σu ) and fatigue strength limit (σ–1) used in this study are extracted from [19 – 23] (refer to the Table).
Fig. 1. Dependence of fatigue strength limit on tensile strength of spring steel:
Mechanical properties of spring steel grades
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The statistical regression model σ–1 = 0.028σu + 566.4 is inadequate. Fisher’s criterion, at 0.206, falls below the significance value (0.657), indicating a low statistical significance. Additionally, the correlation coefficient stands at a meager 0.120.
The results of regression analysis reveal a lack of a meaningful relationship between the function and the parameter. Notably, there’s a noteworthy trend: as the tensile strength of steel escalates, the disparity between actual and calculated results widens.
Consequently, it can be inferred that the factor affecting the reduction of fatigue strength, contingent upon the tensile strength of the metallic matrix (MM), is subject to alteration. Steel products are typically designed considering the fatigue strength of steel. Under these circumstances, it becomes challenging to fully utilize the available strength potential (indicated by high σt and σu levels), thereby limiting the potential to reduce the material intensity of metal structures.
The papers [18; 24] demonstrate that in the non-metallic inclusion – metallic matrix (NMI – MM) system subjected to external impacts, shear stress occurs at their interface within the MM, while NMIs, acting as stress concentrators, have the potential to amplify the effects of these impacts.
Once the stress level attains or surpasses the yield strength under shear (τ), the local regions of the NMI – MM interface activate the Frank-Read sources [16 – 18]. This activation induces local plastic deformation within the metal. With the escalation of dislocation density in these zones, initial cracks begin to propagate, eventually reaching a critical size, thereby instigating material fracture.
The magnitude of resultant shear stresses is assessed using the following equation [18; 24]:
| \[\tau = {\sigma _{\rm{n}}}\frac{{{E_{{\rm{NMI}}}}}}{{{E_{{\rm{ММ}}}}}}\frac{d}{{{l_{\rm{s}}}}},\] | (1) |
where τ is shear stress; σn is external tensile stress; ЕNMI and ЕММ are modulus of elasticity of the NMI and the ММ, respectively; d is diameter (thickness) of the NMI; ls is the sum of maximum lengths of the zone of shear stresses in the MM at the boundary with NMI.
Consequently, the factor \(\frac{{{E_{{\rm{NMI}}}}}}{{{E_{{\rm{ММ}}}}}}\frac{d}{{{l_{\rm{s}}}}}\) represents the stress concentration coefficient (SCС). The equations governing the fatigue strength limit are expressed as follows: \({\sigma _{ - 1}} = \frac{{{\tau _t}}}{{{\rm{SCC}}}}\) or \({\rm{SCC}} = \frac{{{\tau _t}}}{{{\sigma _{ - 1}}}}.\)
In instances where compressive stresses affect the NMI – MM system, shear stresses arise at their interface. However, their magnitude is significantly lower compared to tension scenarios [18]. Henceforth, only tensile forces are further considered.
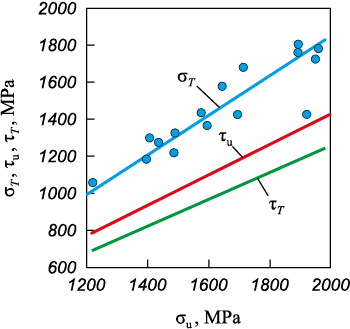
A close statistical association is evident between the yield strength and tensile strength in spring grade steels (Fig. 2). The relationship is mathematically expressed as σТ = 1.08σu – 312, presenting the regression model’s statistical parameters as follows: a standard error of 104.5 MPa; a correlation coefficient of 0.94; Fisher’s criterion standing at 100.86, with a significance level of 9·10\(^–\)8. The dependences of the strength limit, yield strength under shear, and tensile strength of the steel are derived from the equation τ = 0.7 – 0.75σТ .
Fig. 2. Dependences σТ = f (σu); τu = f σu ; τТ = f σu for spring steel grades |
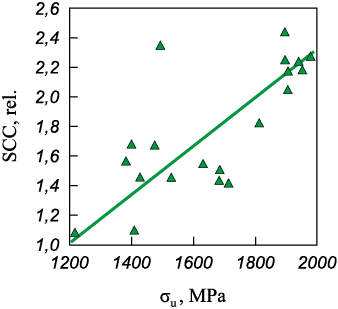
When τ is divided by σТ using the corresponding values of σu , a statistical model of the Stress Concentration Coefficient (SCC) dependency on steel strength is obtained (Fig. 3).
Fig. 3. Dependence of SCC on tensile strength of steel |
The model appears as follows
| SCC = 0.00167σu – 1.04 | (2) |
with statistical parameters indicating a Pearson coefficient is 0.70; a standard error of 0.31; and Fisher’s criterion measuring 15.98, showing a significance level of 0.00093.
Consequently, the SCС exhibits a fairly strong statistical association with the tensile strength of steel. It suggests that as the strength properties increase, so does SCС.
For specific thicknesses of NMIs (d) and their particular morphology, the equation is formulated as follows [18]
| \[{\rm{SCC}} = \frac{{{E_{{\rm{NMI}}}}}}{{{E_{{\rm{ММ}}}}}}\frac{d}{{{l_{\rm{s}}}}} = 2\frac{{{E_{{\rm{NMI}}}}}}{{{E_{{\rm{ММ}}}}}}\frac{{\tau _{\rm{u}}^{{\rm{ММ}}}}}{{\sigma _{\rm{u}}^{{\rm{NMI}}}}},\] | (3) |
where \(\tau _{\rm{u}}^{{\rm{ММ}}}\) represents the MM strength limit during shear and \(\sigma _{\rm{u}}^{{\rm{NMI}}}\) denotes the tensile strength of the NMI.
Results and discussion
The theoretical analysis suggests that when identical NMIs of the same morphological type and the same size coexist within the steel, the relationship between SCC and the steel’s strength properties becomes functional. However, the observed variability in the actual SCС values (Fig. 3) is linked to the presence of diverse morphological types and sizes of NMIs within the metal. The morphology of internally formed NMIs during the steel’s deoxidation process is contingent upon the ratio of oxygen to aluminum dissolved within it [25 – 27]. These endogenous NMIs exhibit varying physical properties, which are notably influenced by the proportion of SiO2 and Al2O3 basic oxides present in them. This variation spans from plastic aluminosilicates to brittle globules, which remain non-deformable during the rolling process, up to yielding pure alumina [28]. Each morphological type of NMI exhibits specific physical and mechanical properties, such as modulus of elasticity (ЕNMI ), tensile strength (\(\sigma _{\rm{u}}^{{\rm{NMI}}}\)) resulting in diverse SCC.
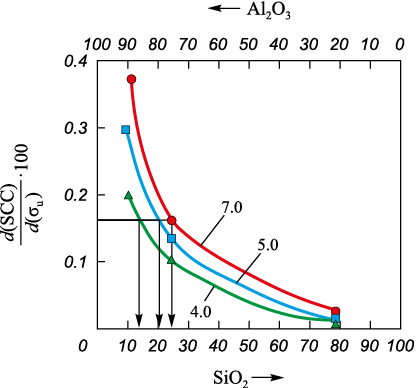
Fig. 4 illustrates the derived relationships depicting the dependency of SCC on the tensile strength of steel concerning three potential elemental compositions of NMIs, %, along with sizes of 4.0, 5.8 and 7.0 μm:
|
Fig. 4. Calculated dependences of SCC on tensile strength |
Aluminosilicates falling within groups 1 and 2 of high-modulus NMIs, surpassing the typical modulus of elasticity within the MM (with an average value of 205 hPa, as indicated in the Table). Conversely, aluminosilicates categorized under group 3 demonstrate low-modulus traits.
SCC escalates proportionally with the increase in both steel strength and the diameter (or thickness) of the NMI. The rate of this rise in SCC depends on the size and elastic modulus ЕNMI of the NMI, dictated by the ratio of mass fractions of SiO2 and Al2O3 oxides within the NMI (Fig. 5). It’s noteworthy that the average rate of change in SCC, calculated from experimental data using Equation (2), corresponds to analogous indicators for NMIs: 13 % SiO2 ; 87 % Al2O3 (4.0 μm thick); 20 % SiO2 , 80 % Al2O3 (5.0 μm thick); 25 % SiO2 ; 75 % Al2O3 (7.0 μm thick).
Fig. 5. Dependence of the rate (intensity) of increase in SCC |
For example, in the context of producing spring grade steels by smelting and deoxidation processes (as indicated in the Table), where diverse high-modulus NMIs are formed, these inclusions significantly impact fatigue indicators. To enhance the steel’s fatigue strength limit, it becomes crucial to ensure the formation of NMIs with a modulus of elasticity not exceeding that of MM (ЕNMI ≤ ЕММ ) and a thickness (d) that does not surpass ls .
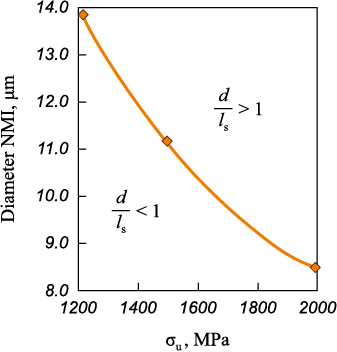
As per [18], achieving involves the formation of NMIs in steel, comprising at least 60 – 65 % SiO2 , with the total content of high-modulus oxides like Al2O3 , MgO not surpassing 35 – 40 %. These NMIs, when produced under these conditions, exhibit ductility at the heating temperature for metal rolling, allowing for easy deformation, resulting in the formation of thin filaments. For example, during rail rolling, aluminosilicate NMIs are generated within the rail head, measuring approximately 4.0 – 6.0 μm in diameter and having an average length of 40 – 50 μm. Fig. 6 illustrates the calculated maximum diameter (or thickness) for NMIs with the specified chemical composition and various levels of tensile strength within the MM.
Рис. 6. Dependence of the limit diameter of NMI (60 – 65 % SiO2 ; |
Hence, as long as the NMI thickness does not exceed 8.5 μm (maintaining a d/ls ≤ 1, ENMI /EММ ≈ 1.0 [18], the SCC remains below 1.0, even with MM strength reaching 2000 MPa. In this context, the fatigue strength of the considered steel must be equal to or exceed the yield strength of the metallic matrix during shear.
Conclusions
To enhance the fatigue endurance of steel, particularly in high-strength conditions, employing aluminum-free metal deoxidation technology during smelting proves beneficial. This approach facilitates the creation of a desirable NMI morphology, ensuring that the SCC remains below 1.0. Achieving a fine-grained structure in steel post heat treatment is feasible by deoxidizing without the inclusion of aluminum, instead incorporating minimal amounts of vanadium, niobium, or titanium.
References
1. Suresh S. Fatigue of metals. Cambridge University Press; 2006:701.
2. Nicholas T. High Cycle Fatigue: A Mechanics of Materials Perspective. Elsevier; 2006:656.
3. Ishida M. Rolling contact fatigue (RCF) defects of rails in Japanese railways and its mitigation strategies. Electronic Journal of Structural Engineering. 2013;13(1):67–74. https://doi.org/10.56748/ejse.131621
4. Zhong W., Hu J.J., Shen P., Wang C.Y., Lius Q.Y. Experimental investigation between rolling contact fatigue and Wear of high-speed and heavy-haul railway and selection of rail material. Wear. 2011;271(9-10):2485–2493.
5. Seo J.-W., Jun H.-K., Kwon S.-J., etc. Rolling contact fatigue and wear of two different rail steels under rolling-sliding contact. International Journal of Fatigue. 2016;83:184–194.
6. Kim D., Quagliato L., Park D., Kim N. Lifetime prediction of linear slide rails based on surface abrasion and rolling contact fatigue-induced damage. Wear. 2019;420-421:184–194. https://doi.org/10.1016/j.wear.2018.10.015
7. Gromov V.E., Ivanov Yu.F., Vorobiev S.V., Konovalov S.V. Fatigue of Steels Modified by High Intensity Electron. Cambridge; 2015:272.
8. Yakovleva T.Yu., Matokhnyuk L.E. Prediction of fatigue characteristics of metals at different loading frequences. Strength of Materials. 2004;36(4):442–448. https://doi.org/10.1023/B:STOM.0000041545.08426.7d
9. Marines-Garcia I., Bin X., Bathias C. An understanding of very high cycle fatigue of metals. International Journal of Fatigue. 2003;25(9-11):1101–1107. http://doi.org/10.1016/S0142-1123(03)00147-6
10. Mylnikov V.V., Shetulov D.I., Chernyshev E.A. On evaluation of durability criteria in carbon steels. Metals Technology. 2010;(2):19–22.
11. Zhao Y., Tan Y., Ji X., Xiang Z., He Y., Xiang S. In situ study of cementite deformation and its fracture mechanism in pearlitic steels. Materials Science and Engineering: A. 2018;731: 93–101. http://doi.org/10.1016/j.msea.2018.05.114
12. Song R., Ponge D., Raabe D. Mechanical properties of an ultrafine grained C–Mn steel processed by warm deformation and annealing. Acta Materialia. 2005;53(18):4881–4792. http://doi.org/10.1016/j.actamat.2005.07.009
13. Calcagnotto M., Adachi Y., Ponge D., Raabe D. Deformation and fracture mechanisms in fine- and ultrafine-grained ferrite/martensite dual-phase steels and the effect of aging. Acta Materialia. 2011;59(2):658–670. http://doi.org/10.1016/j.actamat.2010.10.002
14. Kumar B.R., Raabe D. Tensile deformation characteristics of bulk ultrafine-grained austenitic stainless steel produced by thermal cycling. Scripta Materialia. 2012;66(9):634–637. https://doi.org/10.1016/j.scriptamat.2012.01.052
15. Pavlov V.V., Temlyantsev M.V., Troshkina A.V. On relationship of fatigue parameters with strength properties of steel and the role of non-metallic inclusions. Problemy chernoi metallurgii i materialovedeniya. 2020;(2):44–50. (In Russ.).
16. Evstratova N.N., Kolnaneets V.G., Sukharnikova V.A. Materials Science. Rostov-on-Don: Feniks; 2006:269. (In Russ.).
17. Ardamasova B.N., Mukhina G.G. Materials Science. Moscow: Bauman Moscow State Technical University; 2008:48. (In Russ.).
18. Pavlov V.V. Non-Metallic Inclusions, Fatigue, Contact Fatigue Defects. Novokuznetsk: SibSIU; 2021:144. (In Russ.).
19. Grade Guide of Steels and Alloys. Zubchenko A.S. ed. Moscow: Mashinostroenie; 2003:784. (In Russ.).
20. Metal Science and Heat Treatment of Steel and Cast Iron. In 3 vols. Vol. 1. Methods of Tests and Research. Rakhshtadt A.G., Kaputkina L.M., Prokoshkin S.D., Supov A.V. eds. Moscow: Intermet Inzhiniring; 2004:688. (In Russ.).
21. Metal Science and Heat Treatment of Steel and Cast Iron. In 3 vols. Vol. 3. Thermal and Thermomechanical Treatment of Steel and Cast Iron. Rakhshtadt A.G., Kaputkina L.M., Prokoshkin S.D., Supov A.V. eds. Moscow: Intermet Inzhiniring; 2007:920. (In Russ.).
22. Arzamasov B., Solov’eva T.V., Gerasimov S.A. Handbook of Structural Materials. Moscow: Bauman MSTU; 2005:640. (In Russ.).
23. Sorokin V.G., etc. Steels and Alloys. Grade Guide. Moscow: Intermet inzhiniring; 2001:608. (In Russ.).
24. Pavlov V.V., Korneva L.V. Interaction of the system “metal matrix – non-metal inclusion” in rail steel. In: Sci. Reports “Improving the Quality and Operating Conditions of Rails and Rail Fasteners”. Yekaterinburg; 2010:133–148. (In Russ.).
25. Gubenko S.I. Non-Metallic Inclusions and Strength of Steels. Donetsk: ART-PRESS; 2015:468. (In Russ.).
26. Pavlov V.V. Aluminum-free deoxidation of steel. In: Sci. Reports “Improving the Quality and Operating Conditions of Rails and Rail Fasteners”. Sankt-Peterburg;2015:231–240. (In Russ.).
27. Pavlov V.V., Korneva L.V. Development of a method for assessing the tendency of rail steel to the formation of defects of contact-fatigue origin. In: Sci. Reports “Improving the Quality and Operating Conditions of Rails and Rail Fasteners”. Yekaterinburg; 2011:117–137. (In Russ.).
28. Jiang M., Wang X., Chen B., Wang W. Laboratory study on evolution mechanisms of non-metallic inclusions in high strength alloyed steel refined by high basicity slag. ISIJ International. 2010;50(1):95–104. https://doi.org/10.2355/isijinternational.50.95
About the Authors
V. V. PavlovRussian Federation
Vyacheslav V. Pavlov, Deputy Technical Director
37a Kutuzova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
M. V. Temlyantsev
Russian Federation
Mikhail V. Temlyantsev, Dr. Sci. (Eng.), Prof., Vice-Rector for Educational Work
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
V. V. Bukhmirov
Russian Federation
Vyacheslav V. Bukhmirov, Dr. Sci. (Eng.), Prof., of the Chair of Theoretical Foundations of Thermal Engineering
34 Rabfakovskaya Str., Ivanovo 153003, Russian Federation
Review
For citations:
Pavlov V.V., Temlyantsev M.V., Bukhmirov V.V. Increasing the fatigue strength of high-strength steel grades. Izvestiya. Ferrous Metallurgy. 2023;66(5):522-528. https://doi.org/10.17073/0368-0797-2023-5-522-528