Перейти к:
Метод изучения частотной стабильности материалов при испытаниях на многоцикловую усталость стали
https://doi.org/10.17073/0368-0797-2023-3-367-375
Аннотация
Для безаварийного функционирования и без потерь упругих и неупругих свойств особо ответственных элементов преобразователей электрических колебаний в механические в течение длительного периода циклической наработки необходимо, кроме исследования усталостных характеристик материалов, применяемых для их изготовления, исследовать эти сплавы и на частотную стабильность. Это связано с тем, что незначительные отклонения частоты собственных колебаний приводят к недопустимым погрешностям в работе такого рода высокоточных изделий. Для проведения исследований разработана и сконструирована оригинальная установка, работающая в режиме автоколебаний, в которой осуществлено синусоидальное нагружение плоских образцов по «мягкой» схеме консольного изгиба. Частота циклического нагружения в установке генерируется импульсами тока, которые являются откликом на частоту собственных колебаний испытываемого образца, преобразованных с помощью электроники. В результате достигается частотное равенство в процессе испытаний. Разработан алгоритм расчета напряжений в зависимости от амплитуды нагружения образцов из стали разной геометрической формы. Показано, что напряжение на образце, рассчитанное по амплитуде деформации, во всех случаях на 8 – 10 % выше напряжения, рассчитанного по силе вне зависимости от формы образцов. Для верификации предложенного метода исследований проведены испытания мартенситно-стареющей стали на нагрузках, близких к пределу усталости, так как наибольший интерес представляет стабильность частоты в этом диапазоне. Получены частотные характеристики в многоцикловой области испытаний. Определено, что при наработке в 50 млн циклов нагружения изменение частоты составило 0,75 Гц. Выявлена динамика частотной стабильности: наиболее интенсивно частота менялась при первых 10 млн циклов нагружения, за это время она изменилась на 0,54 Гц.
Ключевые слова
Для цитирования:
Мыльников В.В., Дмитриев Э.А. Метод изучения частотной стабильности материалов при испытаниях на многоцикловую усталость стали. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):367-375. https://doi.org/10.17073/0368-0797-2023-3-367-375
For citation:
Myl’nikov V.V., Dmitriev E.A. A method for studying the frequency stability of materials during tests for multi-cycle fatigue of steel. Izvestiya. Ferrous Metallurgy. 2023;66(3):367-375. https://doi.org/10.17073/0368-0797-2023-3-367-375
Введение
Испытания на усталость материалов проводят с целью определения заданных механических характеристик, применяя стандартные методики испытаний [1]. Используя эти данные, выбирают материал для изготовления требуемых деталей и элементов конструкций, проводят прочностные расчеты [2].
Существует достаточно большое разнообразие циклических испытаний материалов [3 – 6]. Для наиболее точного воспроизведения в образцах напряженного состояния, характерного для конкретных эксплуатационных условий [7 – 10], необходимо выделить из этого многообразия важнейшие параметры усталостного эксперимента:
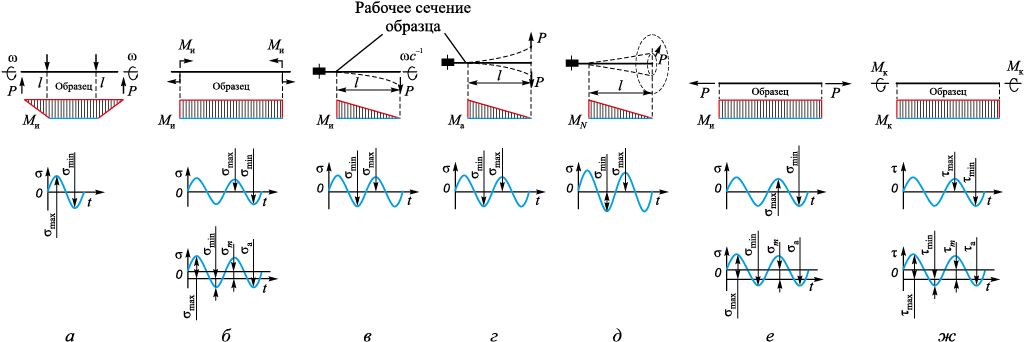
– программа нагружения, определяемая формой амплитудных значений цикла нагружений (рис. 1);
– схема нагружения (рис. 2);
– вид нагружения: мягкое – с заданным размахом нагрузки (σ, МПа) (например, рис. 2, а), жесткое – с заданным размахом деформаций (ε, мм) (например, рис. 2, г).
Рис. 1. Разновидности форм амплитуд циклов:
Рис. 2. Схемы нагружения при испытаниях на усталость: |
В случае конструирования деталей особо ответственного назначения необходимо проводить специализированные узконаправленные испытания материалов, используя вновь создаваемые оригинальные машины и установки с соответствующими экспериментальными методиками.
Так, для изготовления упругих элементов, работающих в сложных условиях циклического нагружения, а также изделий со стабильными размерами требуются материалы с минимальными проявлениями неупругих свойств. В литературных источниках такого рода неупругие свойства при циклическом нагружении имеют различные названия: внутреннего трения, несовершенной упругости, демпфирования, механического гистерезиса, рассеяния энергии, циклической вязкости [11]. В основном такие исследования строятся, исходя из предположения о локализации микропластических деформаций в процессе циклического нагружения, неравномерно возникающих из-за неоднородности различных свойств материала на микроуровне. В других случаях применяют метод динамического механического анализа при изменении температуры для определения предела упругости и энергии активации микромеханизма деформации [12 – 15].
Задача исследования заключалась в разработке экспериментальной методики оценки частотной стабильности материалов для изготовления упругих элементов высокоточных излучателей, преобразующих электрические колебания в механические. В данном случае незначительные изменения частот собственных колебаний, которые связаны с модулем упругости, явлением неупругости и колебанием атомов и их решеток, приводят к недопустимым погрешностям при преобразовании видов колебаний и преждевременному усталостному разрушению [16 – 19].
Материалы и методики исследований
Разработана оригинальная установка (рис. 3) для испытаний по «мягкой» схеме консольного изгиба плоского образца в автоколебательном режиме изотермического циклического нагружения [20]. Установка работает на основе электромеханической системы, в которой возбуждение механических колебаний происходит, исходя из собственной частоты колебания (СЧК) испытуемого образца, т. е. осуществлен режим, когда частота возбуждающей силы или частота циклического нагружения (ЧЦН) всегда равна СЧК образца.
Рис. 3. Схемы: |
Установка содержит три основные части, расположенные раздельно:
– станину, предназначенную для крепления испытываемого образца и электромагнитного возбудителя;
– блок питания и автоматики, предназначенный для питания катушки электромагнитного возбудителя током необходимой величины и частоты;
– средство измерения параметров колебательного процесса и наблюдения за формой колебаний.
Принцип работы установки заключается в следующем. Станина, представляющая собой массивный Г-образный металлический блок, который устанавливается на столе через виброизоляторы, воспринимает колебания образца и передает их пьезоэлектрическому датчику виброускорения. Сигнал с этого датчика поступает в блок питания и автоматики, который, в свою очередь, питает катушку электромагнитного возбудителя генерируемыми импульсами тока частотой, равной СЧК образца. Для исключения наложения волн колебательной энергии и повышения точности их передачи, станина и катушка, собранная совместно со статором одного конца сердечника электромагнитного возбудителя, разделены виброизоляторами в виде виброизоляционных прокладок.
Катушка электромагнитного возбудителя питается пульсирующим током от блока питания (рис. 3, а). При протекании тока возникает электромагнитная сила, под действием которой якорь с образцом движется вниз. При прерывании тока образец под действием силы упругости стремится вернуться в исходное положение. Таким образом осуществляется циклическое нагружение в представленной установке, а полный цикл перемещения нагруженного конца образца в процессе работы демонстрируется на рис. 3, в. При этом СЧК изменяется в процессе усталости материала, что приводит к изменению ЧЦН.
По результатам многократно повторяющихся циклов определены параметры многоцикловой усталости и амплитудно-частотные характеристики для оценки частотных свойств, которые зависят от роли упругой составляющей исследуемого материала при циклическом нагружении, а также предел выносливости. Изменение получаемых частотных показаний может также применяться как мера поврежденности образцов для оценки остаточного ресурса [21].
В установке предусмотрены следующие средства измерения:
– измерение частоты;
– счет числа циклов нагружения;
– измерение амплитуды колебаний оптическим методом;
– измерение амплитуды колебаний фотоэлектрическим методом;
– измерение амплитуды колебаний с помощью пьезоэлектрического датчика виброускорения;
– измерение среднего значения тока в катушке возбудителя;
– наблюдение за колебательным процессом с помощью осциллографа.
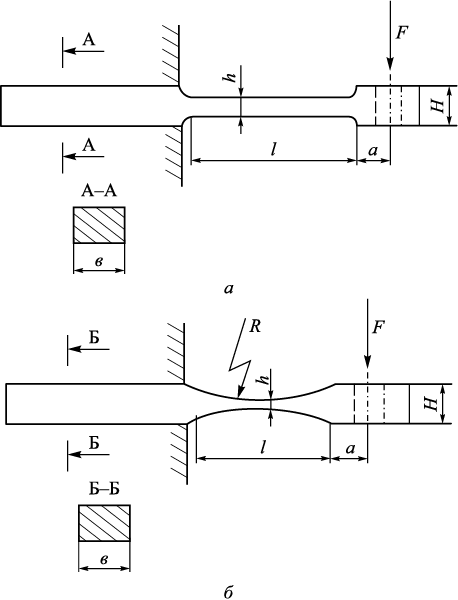
Для испытаний изготавливались образцы из стали 03Н18К9М5Т-ЭЛ, показанные на рис. 4, их размеры приведены в таблице.
Рис. 4. Эскизы образцов:
Размеры образцов для испытания на усталость, мм
|
Напряжение в расчетном сечении образца определяли по амплитуде колебаний. Определение напряжений основано на установлении расчетной зависимости между усилием, прикладываемым к образцу, и его перемещением в точке приложения силы с последующим определением напряжения по известной силе. Установление расчетной зависимости между усилием и перемещением проводится для статического режима. При этом полагается, что в динамическом режиме (в процессе колебаний) действующие на образец силы (внешняя, инерции, упругости) создадут такое же максимальное напряжение и такое же максимальное перемещение (амплитуду колебаний), как и статическая сила, равная по величине результирующей динамической.
При расчете используется приближенное дифференциальное уравнение изогнутой оси балки переменного сечения:
| \[EJ(x)\frac{{{d^2}y}}{{d{x^2}}} = M(x),\] | (1) |
где J(x) – момент инерции сечения; E – модуль Юнга; M(x) – изгибающий момент; y – координата в направлении действия силы; x – координата в направлении оси балки.
Определение соотношения между напряжением и амплитудой колебаний для плоских образцов
Начало координат располагается в месте заделки образца. Момент на расстоянии x от места заделки:
| M = F(l + a – x). | (2) |
Уравнение для перемещения части образца с высотой h: \(\frac{{{d^2}y}}{{d{x^2}}} = \frac{{F(l + a - x)}}{{E{J_1}}},\) где \({J_1} = \frac{{b{h^3}}}{{12}}\).
Начальные условия: x = 0; y1 = 0; \(\frac{{d{y_1}}}{{dx}} = 0\).
Решение с учетом начальных условий:
| \[\left\{ \begin{array}{l}\frac{{d{y_1}}}{{dx}} = \frac{F}{{E{J_1}}}x\left( {l + a - \frac{x}{2}} \right);\\{y_1} = \frac{F}{{E{J_1}}}\frac{{{x^2}}}{2}\left( {l + a - \frac{x}{3}} \right).\end{array} \right.\] | (3) |
Уравнение для перемещения части образца с высотой H: \(\frac{{{d^2}{y_2}}}{{d{x^2}}} = \frac{{F(l + a - x)}}{{E{J_2}}},\) где \({J_2} = \frac{{b{H^3}}}{{12}}\).
Решение уравнения:
| \[\left\{ \begin{array}{l}\frac{{d{y_2}}}{{dx}} = \frac{F}{{E{J_2}}}x\left( {l + a - \frac{x}{2}} \right) + {C_1};\\{Y_2} = \frac{F}{{E{J_2}}}\frac{{{x^3}}}{2}\left( {l + a - \frac{x}{3}} \right) + {C_1}X + {C_2}.\end{array} \right.\] | (4) |
Начальные условия: x = l; \(\frac{{d{y_1}}}{{dx}} = \frac{{d{y_2}}}{{dx}};{\rm{ }}{y_1} = {y_2}\).
Подставив значения x = l в (3) и (4), и решив полученные уравнения, находим:
\[{C_1} = \frac{F}{E}l\left( {\frac{l}{2} + a} \right)\left( {\frac{1}{{{J_1}}} - \frac{1}{{{J_2}}}} \right);{\rm{ }}{C_2} = \frac{F}{E}\frac{{{l^2}}}{2}\left( {\frac{l}{3} + a} \right)\left( {\frac{1}{{{J_1}}} - \frac{1}{{{J_2}}}} \right).\]
Значения постоянных C1 и C2 и уравнение для y2 из (4) позволяют найти максимальное смещение в точке приложения силы при x = l + a:
\[\begin{array}{c}{A_m} = \frac{F}{{E{J_2}}}\frac{{{{(l + a)}^3}}}{3} + \frac{F}{E}l(l + a)\left( {\frac{l}{a} + a} \right)\left( {\frac{1}{{{J_1}}} - \frac{1}{{{J_2}}}} \right) - \\ - \frac{F}{E}\frac{{{l^2}}}{2}\left( {\frac{l}{3} + a} \right)\left( {\frac{1}{{{J_1}}} - \frac{1}{{{J_2}}}} \right).\end{array}\]
При принятых размерах h и H имеет место неравенство J2\( \gg \)J1 (J1 = 208,3 мм4; J2 = 3662 мм4). Учитывая это неравенство и пренебрегая собственным изгибом утолщенной части с высотой H, получим более простое выражение:
| \[{A_m} = \frac{{Fl}}{{E{J_1}}}\left( {{a^2} + la + \frac{{{l^2}}}{3}} \right).\] | (5) |
Напряжение в расчетном сечении (у места заделки): \[\sigma = \frac{{F(l + a)}}{W}\].
Определив F из уравнения (5) и учтя, что \[\frac{{{J_1}}}{W} = \frac{h}{2}\], получим окончательное выражение:
| \[\sigma = \frac{{1,5h(l + a)}}{{l\left( {3{a^2} + 3la + {e^2}} \right)}}E{A_m}.\] | (6) |
Для размеров образца, указанного на рис. 4, а: σ = 26,9·10\(^ - \)5EAm.
При среднем значении модуля Юнга E = 2·105 МПа: σ = 53,8Am, где σ в МПа, Am в мм.
Определение соотношения между напряжением и амплитудой колебаний для корсетных образцов
Рассмотрим отдельно перемещение закругленной части и перемещение утолщенной части.
Для определения перемещения закругленной части расположим начало координат в центре этой части образца, на расстоянии l/2 от места заделки. В этом случае высота сечения, расположенного на расстоянии x от начала координат:
| \[h(x) = h + \left( {R - \sqrt {{R^2} - {x^2}} } \right).\] | (7) |
Момент на расстоянии x: \(M(x) = F\left( {\frac{l}{2} + a - x} \right)\).
Формула для перемещения рассматриваемой части образца получается из уравнения (1) подстановкой значений \({J_1} = \frac{{b{h^3}(x)}}{{12}}\). В свою очередь h(x) берется из уравнения (7).
В результате получаем:
| \[\frac{{{d^2}{y_1}}}{{d{x^2}}} = \frac{{1,5F}}{{bE}}\frac{{0,5l + a - x}}{{{{\left( {0,5h + R - \sqrt {{R^2} - {x^2}} } \right)}^3}}}.\] | (8) |
Значение x лежит в пределах: \( - \frac{l}{2} \le x \le {l_2}\).
Решение дифференциального уравнения (8) с помощью ЭВМ позволяет найти при x = 0,5l: перемещение y1m , угол \({\theta _{1m}} = \frac{{d{y_1}}}{{dx}}\).
Для определения перемещения утолщенной части расположим начало координат на расстоянии l от места заделки образца.
Уравнение для перемещения этой части образца: \(\frac{{{d^2}{y_2}}}{{d{x^2}}} = \frac{{F(a - x)}}{{E{J_2}}}\), где \({J_2} = \frac{{b{H^3}}}{{12}}\).
Решение уравнения:
| \[\left. \begin{array}{r}\frac{{d{y_2}}}{{dx}} = \frac{F}{{E{J_2}}}x\left( {a - \frac{x}{2}} \right) + {C_1};\\{y_2} = \frac{F}{{E{J_2}}}\frac{{{x^2}}}{2}\left( {a - \frac{x}{3}} \right) + {C_1}x + {C_2},\end{array} \right\}\] | (9) |
где 0 ≤ x ≤ a.
Начальные условия: x = 0; \({\theta _{1m}} = \frac{{d{y_2}}}{{dx}}\); y2 = y1m .
Отсюда C1 = θ1m ; C2 = y1m .
Подставив значение x = a в (9), находим значение y2 в точке приложения силы, которое соответствует амплитуде колебаний: \({A_m} = \frac{F}{{E{J_2}}}\frac{{{a^3}}}{2} + {\theta _{1m}}a + {y_{1m}}\).
Ввиду большой величины J2 , первый член этого выражения в тысячи раз меньше двух других и им можно пренебречь.
Обозначим через \({\theta '_{1m}}\) и \({Y'_{1m}}\) значение соответствующих величин, которые определяются из уравнения (9) при \(\frac{{1,5F}}{{bE}} = 1\).
Тогда \({\theta _{1m}} = {\theta '_{1m}}\frac{{1,5F}}{{bE}};{\rm{ }}{y_{1m}} = {y'_{1m}}\frac{{1,5F}}{{bE}}\).
В результате для амплитуды колебаний получим:
| \[{A_m} = \frac{{1,5F}}{{bE}}\left( {{{\theta '}_{1m}}a + {{y'}_{1m}}} \right).\] | (10) |
Напряжение в расчетном сечении в середине закругленной части: \(\sigma = \frac{{F(0,5l + a)}}{W}\).
Определив F из уравнения (10) и учтя, что \(W = \frac{{b{h^2}}}{6}\), получим окончательное выражение:
| \[\sigma = \frac{{2(l + 2a)}}{{{h^2}\left( {{{\theta '}_{1m}}a + {{y'}_{1m}}} \right)}}E{A_m}.\] | (11) |
Задача решена численным методом с помощью ЭВМ. В результате расчета для образцов б1 и б2 с указанными размерами (см. таблица, рис. 4), определено:
– образец б1: \({\theta '_{1m}}\) = 59,84; \({y'_{1m}}\) = 1853,2;
– образец б2: \({\theta '_{1m}}\) = 84,1; \({y'_{1m}}\) = 2532,4.
Из уравнения (11) находим:
– образец (б1): σ = 24,75·10\(^ - \)3EAm, МПа;
– образец (б2): σ = 18,3·10\(^ - \)3EAm, МПа.
При среднем значении модуля Юнга E = 2·105 МПа:
– σ = 49,5Am для образца б1;
– σ = 36,6Am для образца б2.
В вышеприведенных выражениях σ в МПа, Am в мм.
Оценка погрешности определения напряжения в расчетном сечении
Зная погрешности прямого измерения амплитуды колебаний модуля Юнга и геометрических размеров образца, можно рассчитать погрешность косвенного измерения величины σ, воспользовавшись формулой (6)
| \[\frac{{\Delta \sigma }}{\sigma } = {\delta _A} + {\delta _E} + {\delta _e},\] | (12) |
где \({\delta _E} = \frac{{\Delta E}}{E}\) – относительная погрешность определения модуля Юнга; \({\delta _A} = \frac{{\Delta A}}{A}\) – относительная погрешность определения амплитуды;
| \[{\delta _e} = \frac{{\Delta h}}{h} + \left[ {\frac{1}{{a + l}} + \frac{1}{l} + \frac{{2l + 3a}}{{3\left( {{a^2} + ab + \frac{{{l^2}}}{3}} \right)}}} \right]\Delta l + \left( {\frac{1}{{a + l}} + \frac{{l + 2a}}{{{a^2} + al + \frac{{{l^2}}}{3}}}} \right)\Delta a - \] | (13) |
относительная погрешность определения линейных размеров образца.
Относительная погрешность определения амплитуды колебаний определена ранее: δA = 0,01 (1 %).
Относительную погрешность определения линейных размеров образца можно рассчитать по формуле (13):
| δe = 0,0123 (1,23 %). | (14) |
В определении модуля Юнга существует некоторая неопределенность. Литературные данные указывают, что эта величина для высокоупругих сталей может находиться в пределах от 1,9∙105 до 2,1∙105 МПа. Очевидно, в рассмариваемом случае за погрешность в определении модуля Юнга необходимо взять ΔE = ±104 МПа. Тогда получим:
| δE = 0,05 (5 %). | (15) |
Суммарная погрешность определения напряжения в расчетном сечении равна
| \(\frac{{\Delta \sigma }}{\sigma }\) = 0,0723 (7,23 %). | (16) |
В качестве контрольного метода определения напряжения в образце использовался метод статической тарировки, который основан на статическом нагружении образца силой F, измеряемой образцовым динамометром. Напряжение в образце рассчитывалось по известной силе с использованием формулы
| \[\sigma = \frac{{6F(l + a)}}{{b{h^2}}}.\] | (17) |
Одновременно с показаниями образцового динамометра снимались данные измерителя линейных перемещений, определяющего деформацию при нагружении.
Получены следующие значения:
\[\left. \begin{array}{c}{\sigma _A} = 501{A_m} \cdot {10^{ - 6}},{\rm{ Па}},\\{\sigma _F} = \frac{{6(l + a)}}{{b{h^2}}}F = 0,596 \cdot {10^{ - 6}}F,{\rm{ Па;}}\\{\rm{для образца}}{\rm{ а}}\\{\sigma _A} = 485{A_m} \cdot {10^{ - 6}},{\rm{ Па}},\\{\sigma _F} = \frac{{6(l + a)}}{{b{h^2}}}F = 0,444 \cdot {10^{ - 6}}F,{\rm{ Па}}{\rm{.}}\\{\rm{для образца}}{\rm{ б}}\end{array} \right\}\]
Отсюда видно, что напряжения в образцах, определенные по амплитуде деформации и по силе, измеренной образцовым динамометром, отличаются не более, чем на 10 %.
Чтобы оценить этот результат, рассчитаем погрешность определения напряжения в образце по формуле (17). Она складывается из погрешности определения силы \({\sigma _F} = \frac{{\Delta F}}{F}\) и погрешности определения линейных размеров образца \({\sigma _E} = \frac{{\Delta l + \Delta a}}{{l + a}} + \frac{{\Delta b}}{b}\frac{{z\Delta h}}{h}:\)
| \[\frac{{\Delta \sigma }}{\sigma } = {\delta _F} + {\delta _e}.\] | (18) |
При определении размеров образца микрометром Δa = Δl = Δb = Δh = 0,01 мм и погрешность δe = 0,00075 (0,075 %) величина достаточно малая. Основную погрешность вносит процесс измерения силы образцовым динамометром. Эта величина составляет ~1 % и полностью определяет погрешность тарировки.
Напряжение на образце, рассчитанное по амплитуде деформации σA , в обоих случаях на 8 – 10 % выше напряжения, рассчитанного по силе σF как на образцах, показанных на рис. 4, а, так и на образцах, представленных на рис. 4, б. Такое расхождение можно объяснить рядом факторов: погрешностью в определении модуля Юнга, допущениями, сделанными при выводе расчетных формул для σA и неучтенными при тарировке систематическими погрешностями.
Результаты и их обсуждение
В качестве примера применения представленного метода исследования частотной стабильности приведем исследование образца стали 03Н18К9М5Т-ЭЛ (рис. 4, а). Наибольший интерес представляет стабильность частоты при нагрузках, близких к пределу усталости. Поэтому рассмотрим частотные характеристики для образца, который работал с нагрузкой 670 МПа при частоте около 200 Гц. Изменение частоты от начальной в сторону увеличения принято за положительное, в сторону уменьшения – за отрицательное. За контрольное число наработки принято 50 млн циклов нагружения. Максимальное изменение частоты составило 0,75 Гц, что в сравнении с другими образцами показало наилучший результат – самую высокую частотную стабильность. При этом установлено, что наиболее интенсивно частота изменялась при первых 10 млн циклов нагружения, за это время частота изменилась на 0,54 Гц. При непрерывной работе в течение дня образец нарабатывал примерно 10 млн циклов. Частота изменялась при остановке на ночь: утром, после 10-часовой паузы, частота больше, чем накануне вечером при остановке испытаний.
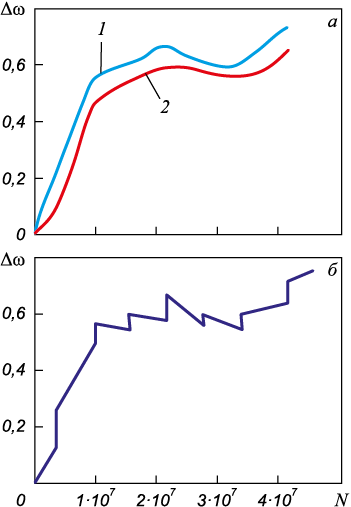
На частотных характеристиках, показанных на рис. 5, а, получены две огибающие кривые, одна из которых (1) соответствует частоте в момент включения, а другая (2) частоте в момент отключения после дневной работы. Следовательно, кривая 1 показывает изменение начальной частоты (частоты включения), а 2 – изменение конечной частоты (частоты отключения). Суточные изменения частоты при наработке циклов лежат в области, ограниченной этими двумя кривыми. На другой частотной характеристике (рис. 5, б) приведена одна ломаная линия. Вертикальные скачки соответствуют изменению частоты после ночного перерыва испытаний. Наклонные линии показывают ход суточного изменения частоты по мере увеличения числа циклов работы.
Рис. 5. Частотные характеристики при циклическом нагружении с перерывами в испытаниях: |
Выводы
Предложен метод и алгоритмы расчета напряжений стальных образцов различной геометрической формы для оценки изменения амплитудно-частотных характеристик в процессе циклического нагружения по схеме поперечного консольного изгиба плоских образцов в режиме «мягкого» нагружения с синусоидальной формой приложения нагрузки. Данный метод является эффективным инструментом для анализа частотный стабильности материала и изменения частот колебаний образца с учетом перерывов испытаний на усталость. Кроме того, по полученным характеристикам несложно определить внутреннее трение материала и внутреннее рассеяние энергии для определения демпфирующей способности материала.
Список литературы
1. Школьник Л.М. Методика усталостных испытаний: Справочник. Москва: Металлургия; 1978:304.
2. Gadolina I.V., Makhutov N.A., Erpalov A.V. Varied approaches to loading assessment in fatigue studies. International Journal of Fatigue. 2021;144:106035. https://doi.org/10.1016/j.ijfatigue.2020.106035
3. Suresh S. Fatigue of Metals. Cambridge University Press; 2006:701.
4. Терентьев В.Ф., Кораблева С.А. Усталость металлов. Mосква: Наука; 2015:479.
5. Gromov V.E., Ivanov Yu.F., Vorobiev S.V., Konovalov S.V. Fatigue of Steels Modified by High Intensity Electron Beams. Cambridge; 2015:272.
6. Mughrabi H., Christ H.-J. Cyclic deformation and fatigue of selected ferritic and austenitic steels; specific aspects. ISIJ International. 1997;37(12):1154–1169. https://doi.org/10.2355/isijinternational.37.1154
7. Gadenin M.M. Study on damaging and fatigue life of constructions under single- and two-frequency loading modes based on deformational and energy approaches. Inorganic Materials. 2018;54(15):1543–1550. https://doi.org/10.1134/S0020168518150049
8. Гаденин М.М. Влияние формы цикла нагружения на сопротивление циклическому деформированию и разрушению конструкционных материалов. Вестник научно-технического развития. 2010;(9(37)):15–19.
9. Мыльников В.В., Шетулов Д.И., Кондрашкин О.Б., Чернышов Е.А., Пронин А.И. Изменение показателей сопротивления усталости конструкционных сталей при различных спектрах нагружения. Известия вузов. Черная Металлургия. 2019;62(10):796–802. https://doi.org/10.17073/0368-0797-2019-10-796-802
10. Гаденин М.М. Расчетно-экспериментальная оценка роли соотношения частот в измерении долговечности при двухчастотных режимах деформирования. Заводская лаборатория. Диагностика материалов. 2019;85(1–1):64–71. https://doi.org/10.26896/1028-6861-2019-85-1-I-64-71
11. Troshchenko V.T., Khamaza L.A., Pokrovsky V.V., etc. Cyclic Deformation and Fatigue of Metals. Bily M. ed. Amsterdam: Elsevier; 1993:500.
12. Головин С.А., Тихонова И.В. Температурная зависимость внутреннего трения и свойства деформированных малоуглеродистых сплавов железа. Деформация и разрушение материалов. 2013;(7):16–21.
13. Головин С.А., Петрушина А.Г. Температурный спектр внутреннего трения чугунов. Известия вузов. Черная металлургия. 2009;52(9):51–54.
14. McClaflin D., Fatemi A. Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effects. International Journal of Fatigue. 2004;26(7):773–784. https://doi.org/10.1016/j.ijfatigue.2003.10.019
15. Головин И.С., Бычков А.С., Михайловская А.В., Добаткин С.В. Вклад фазовых и структурных превращений в многокомпонентных AL-MG сплавах в линейные и нелинейные механизмы неупругости. Физика металлов и металловедение. 2014;115(2):204. https://doi.org/10.7868/ S0015323014020089
16. Kardashev B.K., Sapozhnikov K.V., Betekhtin V.I., Kadomtsev A.G., Narykova M.V. Internal friction, Young’s modulus, and electrical resistivity of submicrocrystalline titanium. Physics of the Solid State. 2017;59(12):2381–2386. https://doi.org/10.1134/S1063783417120204
17. Blanter M.S., Golovin I.S., Neuhäuser H., Sinning H.R. Internal friction in metallic materials. Springer Series in Materials Science. 2007;90:1–535. https://doi.org/10.1007/978-3-540-68758-0
18. Столяров В.В. Неупругость ультрамелкозернистых металлов. Известия вузов. Черная металлургия. 2010;53(11): 51–54.
19. Romaniv O.N., Laz’ko L.P., Krys’kiv A.S. Relationship of internal friction to the fatigue life of patented steel wire. Soviet Mater Science. 1984;19:522–527. https://doi.org/10.1007/BF00722120
20. Пат. 2781466 RU. Установка для испытаний на усталость / Мыльников В.В., Шетулов Д.И.; заявл. 14.09.2021; опубл. 12.10.2022. Бюл. № 29.
21. Демидов А.С., Кашелкин В.В. Определение поврежденности и напряженного состояния балочных образцов по изменению собственной частоты и амплитуды колебаний. Вестник Московского авиационного института. 2009;16(3):62–64.
Об авторах
В. В. МыльниковРоссия
Владимир Викторович Мыльников, к.т.н., доцент кафедры «Технологии строительства»
Россия, 603950, Нижний Новгород, ул. Ильинская, 65
Э. А. Дмитриев
Россия
Эдуард Анатольевич Дмитриев, д.т.н., доцент, ректор
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Рецензия
Для цитирования:
Мыльников В.В., Дмитриев Э.А. Метод изучения частотной стабильности материалов при испытаниях на многоцикловую усталость стали. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):367-375. https://doi.org/10.17073/0368-0797-2023-3-367-375
For citation:
Myl’nikov V.V., Dmitriev E.A. A method for studying the frequency stability of materials during tests for multi-cycle fatigue of steel. Izvestiya. Ferrous Metallurgy. 2023;66(3):367-375. https://doi.org/10.17073/0368-0797-2023-3-367-375