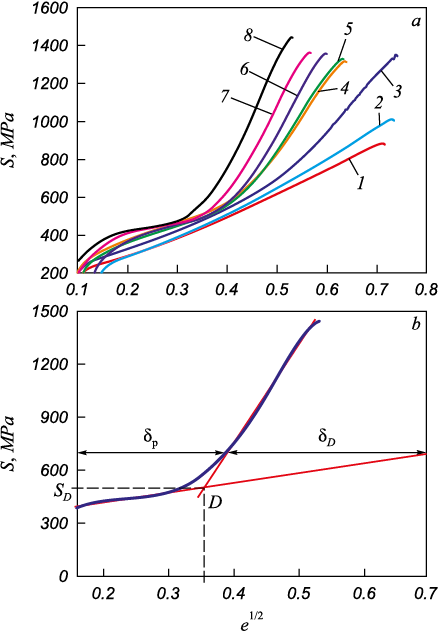Mechanical and acoustic properties of deformable alloys

Introduction

The level of safety in critical objects in atomic power engineering, aircraft, shipbuilding, oil and gas, as well as other industries depends significantly on the effect of resource depletion of design elements of equipment in the operation of structural materials. Therefore, the critical state of material must be forecast, and the physicochemical properties must be monitored before any breaches of its integrity, as well as actual technical state of critical design elements using non-destructive tests. Promising methods of assessment of properties of metals include, inter alia: ultrasound control of material state [1 – 3] exposed to plastic deformation. It is particularly important to study the effect of structural changes on acoustic parameters before the formation of macroscopic cracks. The main factor which significantly influences acoustic parameters is the change in the microheterogeneity upon deformation of materials. These deformations are related to changes in parameters of dislocation structure, density of vacancies, accumulation of micropores and microcracks, inter alia. All these processes influence the rate of ultrasound propagation. This parameter is widely used in the diagnostics of material state [4 – 7]. As previously shown [8 – 10], the change in velocity of ultrasound waves is non-monotonous. In [8] the interrelation between ultrasound velocity and mechanical properties was exemplified by high chromium steel. Regularities of changes in velocity of ultrasound propagation upon variation of composition, structure, and state of metals and alloys were detected and described in details in [11 – 13]. At the same time, the temperature dependences of ultrasound properties must be studied. This includes the range of lower temperatures, since the published data is insufficient [1 – 7].

This work determines the propagation velocity of ultrasound waves V, and the attenuation coefficient α, as a function of total deformation before destruction. It also examines ultimate strength in wide temperature range for austenite stainless steel, grade 12Kh18N10T.

Experimental

The experiments were carried out using crystallites of austenite stainless steel 12Kh18N10T with a grain size of about 12.5 μm. Flat samples with an operational surface area of 40×5×2 mm were exposed to uniaxial tension using an Instron-1185 testing machine at a constant deformation rate of 3.3·10\(^{-}\)⁴ s\(^{-}\)¹. The temperature of tests in the range of 180 K ≤ T ≤ 320 K was preset by purging the working chamber containing deformed sample with nitrogen vapors from Dewar flask, and controlled by Cr/Al thermocouple. The junction was in contact with the sample [14]. The selected temperature range took into account the possibility of achieving forward γ → α′ martensitic transformation in steel [15 – 18].

As the loading curves on the testing rig were measured, the propagation velocity of the Rayleigh surface waves was also measured [19]. The pulses were excited by a piezoelectric converter at a frequency of 5 MHz. The measurement error did not exceed ±3 m/s. The experimental data was processed using the conventional method of statistic analysis. The applied testing rig allowed the information about standard material properties obtained in the course of mechanical tests to be significantly supplemented. These properties were: yield stress, ultimate strength, and coefficient of deformation strengthening. These properties are conditional, reflect weakly the nature of properties running in solids upon deformation and are unrelated to the existing dislocation mechanisms of strengthening [20].

Results and discussion

The tension diagrams in the conditional coordinates of stress (σ) – strain (ε) of steel 12Kh18N10T covered the regions of elastic, plastic deformation and destruction. Then the diagrams were replotted in the coordinates of true stresses (S) – true strains (e) [20] and in the function S(e^1/2) with the detection of the bending points on them (Fig. 1, a) located between the yield stress and the ultimate strength. These critical points indicate transition from elastic plastic to plastic destruction stage of deformation. This is interrelated with accumulation of microdamages in steel. The critical point D in the diagram corresponds to the stress S_D and the strain e_D (Fig. 1, b). They can be considered critical parameters for provision of maximum operability of metal in the considered temperature range.

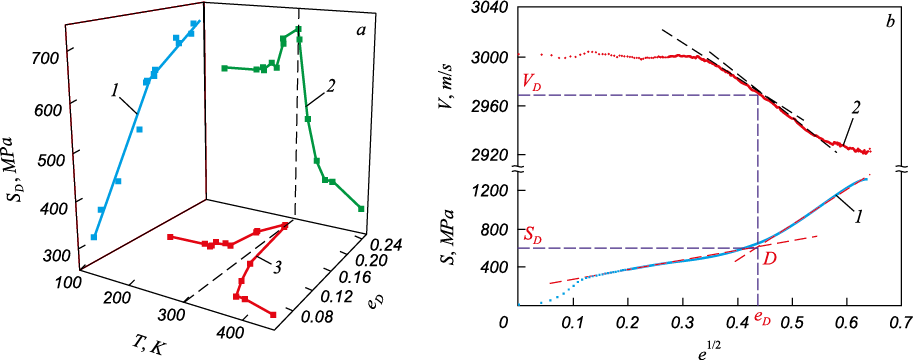
Fig. 2, a illustrates dependences of deformation strength properties corresponding to the point D: S_D(e_D) (curve 1), S_D(T) (curve 2) and e_D(T) (curve 3). The temperature dependences of deformation strength properties demonstrate an extreme pattern. For all points D the critical parameter Δ = δ_D/δ_p can be calculated (where δ_p is the elastic plastic constituent in relative elongation before rupture. δ_D is the plastic destruction constituent in relative elongation before rupture) (Fig. 1, b).

Fig. 2, b combines the diagram S(e^1/2) (curve 1) and measured velocities of ultrasound propagation V(e^1/2) (curve 2), as a function of total deformation. Point D is also shown corresponding to the critical ultrasound velocity V_D. A decrease in the testing temperature during tension of steel samples leads to an increase in the density of defects and growth of martensitic phase. Thus, as a consequence, in leads to an increase in local stresses (stresses of the 2^nd kind). All this is reflected by a decrease in the ultrasound velocity with an increase in total deformation and acting stresses. Achievement of the ultrasound velocity V = V_D at the considered temperatures indicates transition from elastic plastic to plastic destruction stage of deformation.

The processing of changes in the velocity of ultrasound propagation at various temperatures for fixed values of total plastic deformation allowed linear pattern of V(T) dependence with the correlation coefficient R = 0.97 to be established. With a decrease in the testing temperature in the considered range, the change in ultrasound velocity reaches 20 % in the non-deformed sample, and 15 % in the deformed sample (at total deformation of 0.3), in comparison with the ultrasound velocity in the non-deformed material at ambient temperature.

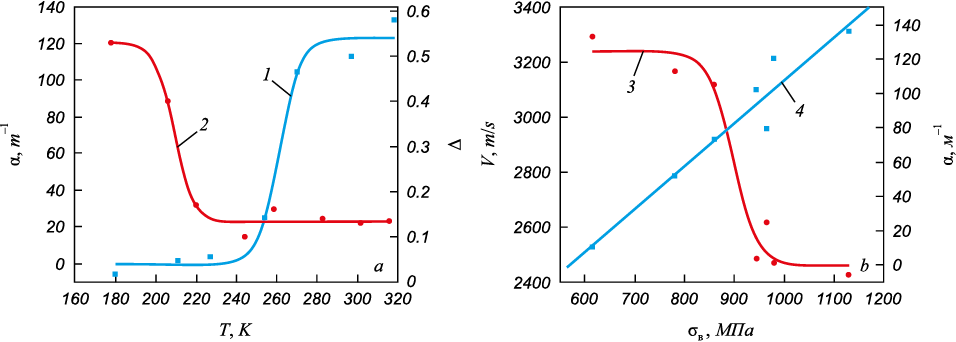
Fig. 3, a illustrates temperature sigmoidal dependences of the coefficient of ultrasound attenuation α(T) (curve 1), corresponding to the point D, and the critical parameter Δ(T) (curve 2). It was also established that in the deformable samples, the coefficient of ultrasound attenuation as a function of ultimate strength α(σ_u) is of sigmoidal shape (Fig. 3, b). However, the ultrasound velocity as a function of ultimate strength V(σ_u) is linear in the temperature range considered. Stresses corresponding to the maximum rate of increase in volumetric fraction of martensitic α′ phase and decrease in the ultrasound velocity were determined.

Mechanical uniaxial tensile tests of steel samples demonstrated that a decrease in the testing temperature results in an increase in yield stress. The ultimate strength against the background of plasticity decreases. The linear pattern of the ultrasound velocity as a function of ultimate strength V(σ_u) is probably stipulated by the functional interrelation of the ultimate strength σ_u with elastic properties of steel. Since the velocity of transversal ultrasound waves is V  = (G/ρ)^1/2 (where G is the modulus of shift; ρ is the density), then the difference of the elasticity moduli of increasing martensitic phase upon γ → α′ martensitic transformation during plastic deformation [15] from the moduli of steel matrix leads to changes in elastic and acoustic properties of overall alloy.

Therefore, on the basis of velocities of ultrasound propagation and the attenuation coefficient, it is possible to forecast ultimate strength and maximum operability of a considered metal at low temperatures. It is thus assumed that fulfillment of the condition e < e_D indicates that the current deformation corresponds to the elastic plastic constituent δ_p and Δ → 0. This is as a consequence of fabrication or operation of the item Δ ≠ 0, which is evidence that the material is already operating in the plastic destruction stage.

Conclusions

The study determined that tension of samples of austenite stainless steel, Grade 12Kh18N10T, in the temperature range of 180 K ≤ T ≤ 320 K leads to significant changes in ultrasound velocity. The temperature dependences of ultrasound velocity, attenuation coefficient, yield stress and ultimate strength were established. The critical parameters of transition from elastic plastic to plastic destruction stage of deformation were determined. The correlations between the parameters provide evidence that it is possible to obtain regression dependences between them, and this can be used for recovery of one property on the basis of other determined experimentally. Among all such pairs of dependences, of most practical interest are the interrelations between the pairs of mechanical and acoustic parameters. Since measurements of the latter is less labor-consuming, they can be measured directly on analyzed element during operation without destruction, and the experiments do not require fabrication of samples.