Scroll to:
Simulation of slab heating in a walking beam furnace
https://doi.org/10.17073/0368-0797-2023-1-112-118
Abstract
Slabs are preheated before hot rolling to achieve the required metal plasticity. Walking beam furnace is the most efficient form of equipment since it heats the slab from all sides. Nevertheless, the bottom surfaces in contact with the water-cooled support beams are shielded from the heat radiated by the lower part of the furnace, and their heat is transferred to the beams. We developed and implemented by means of software a simulation model to study the non-uniformity of the temperature distribution across the slab and how the slab transportation system design affects it. Thesimulation model includes a numerical solution of a 3D thermal conductivity problem with piecewise defined boundary conditions on the slab bottom surface. Identical boundary conditions were applied to both the top surface and the open areas of the slab bottom surface. For the areas of contact with the beams, we applied modified boundary conditions to account for the duration of the contact. We numerically solved the system of difference equations with the layer-by-layer method, in order to obtain a system defined by a tridiagonal matrix. The slab-to-beam contact heat transfer was assumed to be adiabatic during the entire contact period. The calculations produced the temperature fields at different cross-sections of the slab. As a result, we discovered a significant non-uniformity of the temperature field on the lower surface of the slab leading to the entire temperature field non-uniformity of the slab. We developed simulation and visualization software to study the slab temperature field under various heating conditions. The simulation model is refined from the experimental data available.
Keywords
For citations:
Abdukodirov I.B., Vargin A.V., Levitskii I.A. Simulation of slab heating in a walking beam furnace. Izvestiya. Ferrous Metallurgy. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
Introduction
The walking beam furnace providing slab heating from four sides is a state-of-the-art piece of equipment. It preheats slabs before hot rolling [1]. The slab movement system in such furnaces contains fixed and movable beams which partially shield the contact areas of the bottom surface of the slab from the thermal radiation of the combustion products coming from the lower heating area. It leads to partial heat outflow through heat conduction in the contact areas. The experimental study of heat transfer in industrial conditions is challenging, so we used simulation instead. The models simulating metal heating in furnaces [2, 3] can be divided into statistical [4, 5], analytical [6], and numerical [7 – 10]. Both direct and inverse heat conduction problems are considered in some articles [6, 11]. Simulation of in-furnace processes is extensively used to solve optimization problems [11 – 15] or to employ the capabilities of with advanced CFD software [16, 17].
The purpose of this study is to build a simulation model of slab heating in a walking beam furnace that accounts for the effect of these beams on the heating and apply the model to analyze the temperature field of the slab.
Methods and Materials
The simulation model addresses a 3D unsteady heat conduction problem in the Cartesian coordinate system. The computational domain is a parallelepiped without any internal heat sources. Its thermophysical properties are temperature-dependent. The model uses asymmetric boundary conditions of the third kind. These conditions are piecewise on the bottom surface of the computational domain.
With the above assumptions, the heat conduction equation is nonlinear:
| \(\begin{array}{c}\frac{{\partial T}}{{\partial t}} = \frac{1}{{{\rm{\rho }}c}}\left[ {\frac{\partial }{{\partial x}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial z}}} \right)} \right]{\rm{, }}\\\left\{ {{\rm{0}} < x < {{\rm{\delta }}_x},{\rm{0}} < y < {{\rm{\delta }}_y},{\rm{ 0}} < z < {{\rm{\delta }}_z}} \right\}\end{array}\). | (1) |
The initial temperature field is homogeneous
| T(x, y, z) = Tb . | (2) |
Then the boundary conditions can be expressed as:
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right)} \right|_{x = 0}} = \alpha _x^ \uparrow \left( {{T_{\rm{g}}} - {T_{x = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right)} \right|_{x = {\delta _x}}} = \alpha _x^ \downarrow \left( {{T_{\rm{g}}} - {T_{x = {\delta _x}}}} \right);\end{array}\); | (3) |
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right)} \right|_{y = 0}} = \alpha _y^ \uparrow (z)\left( {T_{\rm{g}}^ \uparrow (z) - {T_{y = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right)} \right|_{y = {\delta _y}}} = \alpha _y^ \downarrow \left( {{T_{\rm{g}}} - {T_{y = {\delta _y}}}} \right)\end{array}\); | (4) |
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right)} \right|_{z = 0}} = \alpha _z^ \uparrow \left( {{T_{\rm{g}}} - {T_{z = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right)} \right|_{z = {\delta _z}}} = \alpha _z^ \downarrow \left( {{T_{\rm{g}}} - {T_{z = {\delta _z}}}} \right)\end{array}\). | (5) |
Eq. (1) – (5) is a complete formulation of the differential heat conduction problem. The notations are defined as follows: T(x, y, z, t) is the slab temperature, K; δx , δy , δz are the slab dimensions (width, thickness, length), m; ρ is the slab material density, kg/m3; с is slab material specific heat capacity, J/(kg∙K); λ is the slab material thermal conductivity, W/(m·K); \(\alpha_x^\uparrow\) and \(\alpha_x^\downarrow\) are the heat transfer coefficients on the rear and front vertical surfaces of the slab, respectively, W/(m2∙K); \(\alpha_y^\uparrow\) and \(\alpha_y^\downarrow\) are the heat transfer coefficients on the bottom and top surfaces of the slab, respectively, W/(m2∙K); \(\alpha_z^\uparrow\) and \(\alpha_z^\downarrow\) are the heat transfer coefficients on the left and right end surfaces of the slab, respectively, W/(m2∙K); Тг is the heating medium temperature, K; Tb is initial slab temerature, K.
The equations are expressed in the coordinate system attached to the slab. For this reason, the design features of a specific furnace affect the boundary conditions. First, in order to account for different heating conditions in various furnace areas, the heat transfer coefficients and the temperature of the heating medium are described as a piecewise function of time. Secondly, the properties are specified individually for each slab surface to take into account the furnace geometry in the simulation model. For example, if the furnace hearth is solid (which is common in walking hearth and pusher furnaces), the respective heat transfer coefficient \(\alpha_y^\uparrow\) is set to zero. In this way, we expressed the adiabatic condition on the slab bottom surface. For walking beam furnaces, the boundary conditions at the slab top and bottom surfaces must be consistent with the different heat input rates in the lower and upper areas of the furnace chamber. Although the combustion occurs in both lower and upper areas, the slab bottom surface is significantly shielded by the slab transport components. Moreover, the slab bottom surface has contact areas with riders on the movable and fixed beams. For this reason, the boundary conditions should be different for the three types of bottom surface areas:
– areas between the beams (type 0);
– areas that periodically come into contact with the movable beams (type 1);
– areas in permanent contact with the fixed beams (type 2).
This means that \(\alpha _y^ \uparrow (z)\) and \(T_{\rm{g}}^ \uparrow (z)\) – members of the boundary conditions on the slab bottom surface – are piecewise functions of the coordinate along the slab’s length. They are piecewise functions of time in the same way as the other boundary conditions. We also should remember that as the slab is walked (moved) through the furnace, both the contact conditions with the beams and the intensity of the slab bottom surface shielding vary. The simulation model describes the heat transfer on the slab bottom surface as it comes into contact with the cooled beam by the conditional heat transfer coefficients \({\tilde \alpha _{\rm{s}}}\) and \({\tilde \alpha _{\rm{m}}}\), W/(m2∙K). The heat is transferred to the medium at a temperature \({\tilde T_{\rm{s}}}\) or \({\tilde T_{\rm{m}}}\), K, which circulates in the beam cooling system. In most cases, the coolant is water or steam. For open-flame furnaces (they also include walking beam furnaces), the heat transfer coefficients describe both convective and radiative heat transfer (linearization of the (3) – (5) boundary conditions is beneficial to accelerate the numerical solution convergence).
The walking cycle consists of individual stages. We used the stage names and approximate durations specified in the datasheet of a furnace operated in Casthouse No. 2, Severstal. The walk beam system specifications are listed in Table 1.
Table 1. Example of the walking mechanism characteristics
|
Note that the information in Table 1 is insufficient to estimate the slab-to-beam contact time. We need to know the slab feed cycle time τ, s (its minimum value is equal to the total duration of walking, but in real-life applications, the value is usually several times greater), and the spacing between the slabs in the furnace L, m (sum of the slab width and the slab-to-slab gap). Then during the feed cycle τ, the time of contact with the movable beams is [7]:
| \({{\rm{\tau }}_{\rm{m}}} = \frac{L}{l}\left( {{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }} \right)\), | (6) |
and the time of contact with the stationary beams is
| \({{\rm{\tau }}_{\rm{s}}} = {\rm{\tau }} - \frac{L}{l}\left( {{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }} \right)\). | (7) |
For heating simulation, modifying the boundary conditions at each walking stage is impractical, because it would require extremely small time steps (Δt ≤ 1 с). It is advisable to specify the boundary conditions for the areas in contact with the beams as a weighted average result to account for the share of total contact time. This approach does not require the time steps to be multiples of the walking stage durations. Then the effective heat transfer coefficient, specified as a boundary condition on an area of the lower surface of an i th type, is estimated as
| \[\alpha _y^ \uparrow ({z_i}) = \left\{ {\begin{array}{*{20}{c}}{{\alpha ^ \uparrow },}\\{{\alpha ^ \uparrow }\left( {1 - \xi } \right) + \xi {{\tilde \alpha }_{\rm{m}}},}\\{{\alpha ^ \uparrow }\xi + {{\tilde \alpha }_{\rm{m}}}\left( {1 - \xi } \right),}\end{array}\begin{array}{*{20}{c}}{i = 0}\\{i = 1}\\{i = 2}\end{array}} \right.\], | (8) |
the effective temperature of the medium in contact with the lower surface area of the i th type is
| \(T_{\rm{g}}^ \uparrow ({z_i}) = \large \left\{ \begin{array}{l}{T_{\rm{g}}},{\rm{ }}i = 0\\\frac{{{\rm{\xi }}{{{\rm{\tilde \alpha }}}_{\rm{m}}}{{\tilde T}_{\rm{m}}} + \left( {1 - {\rm{\xi }}} \right){{\rm{\alpha }}^ \uparrow }{T_{\rm{g}}}}}{{{\rm{\xi }}{{{\rm{\tilde \alpha }}}_{\rm{m}}} + \left( {1 - {\rm{\xi }}} \right){{\rm{\alpha }}^ \uparrow }}}{\rm{, }}i = 1\\\frac{{\left( {{\rm{1}} - {\rm{\xi }}} \right){{{\rm{\tilde \alpha }}}_{\rm{s}}}{{\tilde T}_{\rm{s}}} + {\rm{\xi }}{{\rm{\alpha }}^ \uparrow }{T_{\rm{g}}}}}{{\left( {{\rm{1}} - {\rm{\xi }}} \right){{{\rm{\tilde \alpha }}}_{\rm{s}}} + {\rm{\xi }}{{\rm{\alpha }}^ \uparrow }}}{\rm{, }}i = 2\end{array} \right.\), | (9) |
the auxiliary coefficient ξ characterizes the share of time when the slab is in contact with the movable beams:
| \({\rm{\xi }} = \frac{{{{\rm{\tau }}_{\rm{m}}}}}{{\rm{\tau }}} = \frac{L}{l}\frac{{{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }}}{{\rm{\tau }}}\). | (10) |
The non-linear problem (1) – (5) has no analytical solution, so we had to resolve it by the finite difference method [7, 18, 19].
This method introduces a discrete time variable tk = kΔt (k = 1, 2, ...) with the constant step Δt and discrete coordinates xi = iΔx (i = 0, 1, 2, .., nx ), yj = jΔy (j = 0, 1, 2, .., ny ), zl = lΔz (l = 0, 1, 2, .., nz ). For the simple geometry under consideration, the coordinate also changes with the constant steps Δx, Δy and Δz. The nx , ny and nz values are the numbers of partitions along each coordinate axis.
As a result, the computational domain is partitioned into elementary volumes. Their number is equal to (nx + 1)(ny + 1)(nz + 1). Each of these elementary volumes contains one node of the 3D grid. Each node is denoted with three indices (i, j, l). At each time step increment, the heat balance equations are formulated for each elementary volume. They form a quasi-linear system of equations where the temperatures at the nodes at the end of each time step are unknown quantities. Solving the system with general methods is not advisable [19, 20].
Results
We implemented the simulation model as a Builder C++ ver. 6.0 application. The software supports three algorithms for solving the system of difference equations:
– the split method (applicable to linear problems only);
– the simple iteration method (low memory requirements, but slow to converge);
– the layer-by-layer method (direct solution for heat propagation along the slab thickness with an iterative refinement of its propagation along the length and width).
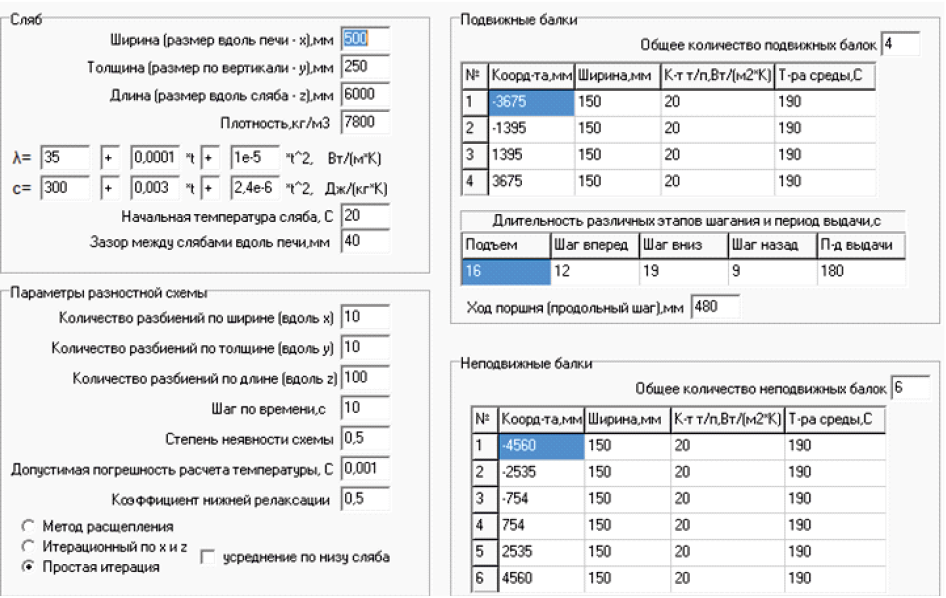
The \({\tilde \alpha _{\rm{s}}}\), \({\tilde \alpha _{\rm{m}}}\), \({\tilde T_{\rm{s}}}\), \({\tilde T_{\rm{m}}}\) values can be found only from test data using a model of heat transfer between the slab bottom surface and the slab transport components. For our software implementation, these values are input data. So far we proposed to take into account only the shielding effect of the slab transport components by setting \({\tilde \alpha _{\rm{s}}}\) and \({\tilde \alpha _{\rm{m}}}\) to zero. Fig. 1 shows the initial data for the simulation, and Table 2 lists the slab heating conditions in a five zone heating furnace.
Fig. 1. Input data for simulation |
Table 2. Simulated heating conditions
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The heat balance of the slab is verified at each time step and globally (max error does not exceed 0.001). Fig. 2 shows the final temperature profiles for the bottom (a) and top (b) surfaces (temperature variation along the longitudinal axis of the surface) of a 250×500×6000 mm slab heated in a furnace with four fixed and two movable beams. For comparison, Fig. 2, c shows the temperature profile along the axis of the bottom surface heated under uniform boundary conditions obtained by averaging of conditions at this surface.
Fig. 2. Temperature profile along the axis of the top (а) and bottom (b) slab surfaces |
Discussion
The results indicate that at the slab end faces, the temperature on the axis of the top and bottom surfaces increases by about 20 – 25 °C regardless of the type of boundary conditions. This can be explained by the effect of heat supply to the slab ends. In terms of the uniform boundary conditions on the bottom surface, the temperature profile in the rest of the bottom surface axis of the slab is virtually uniform (Fig. 2, c), while for piecewise boundary conditions, the temperature field non-uniformity in this area reaches 48 °C (Fig. 2, a). The non-uniformity of the temperature field can also be seen at the slab top face, but it is significantly lower (about 15 °C away from the slab ends, refer to Fig. 2, b). It should also be noted that for stationary beams, the “impact spot” is deeper and wider than for movable beams (Fig. 2, a). This is because the contact time of the slab bottom surface with the stationary beams is longer than with the movable beams.
The software can be used to study the slab temperature field in various heating conditions from available experimental data used to specify the model tuning parameters \({\tilde \alpha _{\rm{s}}}\), \({\tilde \alpha _{\rm{m}}}\), \({\tilde T_{\rm{s}}}\) and \({\tilde T_{\rm{m}}}\). The results of analysis when only the shielding effect of the beams is accounted for should be considered as a lower-bound estimate of the slab temperature field non-uniformity.
Conclusions
We developed and implemented a simulation model of the slab heating in a walking beam furnace which accounts for the effect of the beams on the slab bottom surface.
The model is a 3D unsteady thermal conductivity problem with boundary conditions of the third kind. These conditions are piecewise on the slab bottom surface.
For a furnace with four fixed and two movable beams, we simulated the heating of a 250×500×6000 mm slab under standard conditions and accounting for only the shielding effect of the beams on the slab bottom surface. The temperature non-uniformity on the slab bottom surface away from its ends was about 48 °C, while on the top surface – about 15 °C.
References
1. Gusovskii V.L., Lifshits A.E. Methods of Heating and Thermal Furnaces Design: Reference Textbook. Moscow: Teplotechnik; 2004: 400. (In Russ.).
2. Timoshpol’skii V.I., Trusova I.A., Mendeleev D.V., Ratnikov P.E. Analysis of mathematical modeling methods of heat transfer in industrial furnaces for metal heating. Lit’e i metallurgiya. 2012; 2(65): 102–107. (In Russ.).
3. Singh V.K., Talukdar P. Comparisons of different heat transfer models of a walking beam type reheat furnace. International Communications in Heat and Mass Transfer. 2013; 47: 20–26. https://doi.org/10.1016/j.icheatmasstransfer.2013.06.004
4. Belen’kiy A.M., Bogatova M.Zh., Chibizova S.I. Statistical modeling of metal heating in furnaces with walking beams. Chernye Metally. 2021; 8: 32–37. (In Russ.). https://doi.org/10.17580/chm.2021.08.06
5. Bogatova M.Zh., Chibizova S.I. Statistical modeling of temperature operating modes of heating furnaces for hot strip mills. Izvestiya. Ferrous Metallurgy. 2021; 64(5): 374–381. (In Russ.). https://doi.org/10.17073/0368-0797-2021-5-374-381
6. Levitskiy I.A. The linear heat conduction problem for bodies with a regular shape under boundary conditions of the third kind. Chernye Metally. 2019; 10: 67–72. (In Russ.).
7. Abdukodirov I.B. Mathematical model of slab heating in a furnace with walking beams: Mag. Diss. Moscow; 2020: 68. (In Russ.).
8. Han S.H., Chang D., Kim C.Y. A numerical analysis of slab heating characteristics in a walking beam type reheating furnace. International Journal of Heat and Mass Transfer. 2010; 53(19-20): 3855–3861. https://doi.org/10.1016/j.ijheatmasstransfer.2010.05.002
9. Kurnosov V.V., Levitskii I.A., Pribytkov I.A. Massive billets different rates heating in batch furnaces study. Izvestiya. Ferrous Metallurgy. 2012; 55(9): 27–31. (In Russ.). https://doi.org/10.17073/0368-0797-2012-9-27-31
10. Landfahrer M., Schluck C. Numerical and experimental investigation of scale formation on steel tubes in a real-size reheating furnace. International Journal of Heat and Mass Transfer. 2019; 129: 460–467. https://doi.org/10.1016/j.ijheatmasstransfer.2018.09.110
11. Kurnosov V.V., Levitskii I.A. Mathematic simulation of workpieces heating with variable thermal characteristics and thermal condition, corresponding to a given heating curve. Izvestiya. Ferrous Metallurgy. 2012; 55(7): 19–22. (In Russ.). https://doi.org/10.17073/0368-0797-2012-7-19-22
12. Jang J.-Y., Huang J.-B. Optimization of a slab heating pattern for minimum energy consumption in a walking-beam type reheating furnace. Applied Thermal Engineering. 2015; 85: 313–321. https://doi.org/10.1016/J.APPLTHERMALENG.2015.04.029
13. Tang G., Wu B., Bai D., Wang Y., Bodnar R., Zhou C.Q. Modeling of the slab heating process in a walking beam reheating furnace for process optimization. International Journal of Heat and Mass Transfer. 2017; 113: 1142–1151. https://doi.org/10.1016/j.ijheatmasstransfer.2017.06.026
14. Ding J.G., Kong L.P., Guo J.H., Song M.X., Jiao Z.J. Multi-objective optimization of slab heating process in walking beam reheating furnace based on particle swarm optimization algorithm. Steel Research International. 2021; 92(3): 2000382. https://doi.org/10.1002/srin.202000382
15. Tang L., Liu J., Rong A., Yang Z. An effective heuristic algorithm to minimise stack shuffles in selecting steel slabs from the slab yard for heating and rolling. Journal of the Operational Research Society. 2001; 52(10): 1091–1097. https://doi.org/10.1057/palgrave.jors.2601143
16. Tang G., Wu B., Wang Y., Bodnar R., Zhou C. CFD modeling and validation of a dynamic slab heating process in an industrial walking beam reheating furnace. Applied Thermal Engineering. 2018; 132: 779–789. https://doi.org/10.1016/j.applthermaleng.2018.01.017
17. Mayr B., Prieler R., Demuth M., Moderer L., Hochenauer C. CFD analysis of a pusher type reheating furnace and the billet heating characteristic. Applied Thermal Engineering. 2017; 115: 986–994. https://doi.org/10.1016/j.applthermaleng.2017.01.028
18. Arutyunov V.A., Bukhmirov V.V., Krupennikov S.A. Mathematical Modeling of Industrial Furnaces Thermal Operation. Moscow: Metallurgiya; 1990: 239. (In Russ.).
19. Kudinov V.A., Kudinov I.V. Methods for Solving Parabolic and Hyperbolic Equations of Heat Conduction. Moscow: Librokom; 2012: 280. (In Russ.).
20. Mathews J.H. Computer derivations of numerical differentiation formulae. International Journal of Mathematics Education in Science and Technology. 2003; 34(2): 280–287. https://doi.org/10.1080/0020739031000158317
About the Authors
I. B. AbdukodirovRussian Federation
Ilkhomzhon B. Abdukodirov, Deputy Head of the Section of Metal Preparation and Sorting
41 Kh. Baikaro Str., Tashkent 100213, Republic of Uzbekistan
A. V. Vargin
Russian Federation
Aleksandr V. Vargin, Postgraduate of the Chair “Energy-Efficient and Resource-Saving Industrial Technologies”
4 Leninskii Ave., Moscow 119049, Russian Federation
I. A. Levitskii
Russian Federation
Igor’ A. Levitskii, Cand. Sci. (Eng.), Assist. Prof. of the Chair “Energy-Efficient and Resource-Saving Industrial Technologies”
4 Leninskii Ave., Moscow 119049, Russian Federation
Review
For citations:
Abdukodirov I.B., Vargin A.V., Levitskii I.A. Simulation of slab heating in a walking beam furnace. Izvestiya. Ferrous Metallurgy. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
JATS XML