Содержание
Перейти к:
Математическая модель нагрева сляба в печи с шагающими балками
https://doi.org/10.17073/0368-0797-2023-1-112-118
Аннотация
Нагрев слябов перед горячей прокаткой необходим для придания металлу требуемых пластических свойств. Наиболее эффективны для этого печи с шагающими балками, обеспечивающие подачу теплоты со всех сторон сляба. Однако области нижних поверхностей слябов, контактирующие с водоохлаждаемыми балками, экранированы от излучения нижних зон обогрева печи и отдают теплоту балкам. Для исследования неоднородности температурного поля слябов и ее зависимости от особенностей конструкции системы транспортировки разработана и программно реализована математическая модель нагрева сляба в печи с шагающими балками. Модель основана на численном решении трехмерной задачи теплопроводности с кусочно-определенными граничными условиями на нижней поверхности сляба. Для открытых областей нижней поверхности сляба задавались такие же граничные условия, как на верхней поверхности, а для областей контакта с балками – модифицированные граничные условия, учитывающие продолжительность этого контакта. Для численного решения системы разностных уравнений применен послойный метод, позволяющий получить систему с трехдиагональной матрицей коэффициентов. Проведенные расчеты в приближении адиабатности участков контакта сляба с балками в период контакта позволили получить температурные поля для различных сечений сляба. В результате выявлена существенная неоднородность температурного поля нижней поверхности сляба, влияющая на неоднородность температурного поля всего сляба. Разработанная программа расчета и визуализации результатов может быть использована для изучения температурного поля сляба при различных режимах его нагрева в случае наличия экспериментальной информации, позволяющей уточнить настроечные параметры модели.
Ключевые слова
математическое моделирование,
нагрев сляба,
печь с шагающими балками,
трехмерная задача теплопроводности,
граничные условия,
метод конечных разностей,
коэффициент теплоотдачи
Для цитирования:
Абдукодиров И.Б., Варгин А.В., Левицкий И.А. Математическая модель нагрева сляба в печи с шагающими балками. Известия высших учебных заведений. Черная Металлургия. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
For citation:
Abdukodirov I.B., Vargin A.V., Levitskii I.A. Simulation of slab heating in a walking beam furnace. Izvestiya. Ferrous Metallurgy. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
Введение
Наиболее прогрессивными агрегатами в производстве горячекатаного листа, используемыми для нагрева слябов перед прокаткой, являются печи с шагающими балками, обеспечивающие четырехстороннюю схему нагрева [1]. Применяемая в этих печах система транспортировки слябов содержит стационарные и подвижные балки, которые частично экранируют контактирующие с ними области нижней поверхности сляба от теплового излучения продуктов сгорания нижних зон обогрева, а частично приводят к оттоку теплоты теплопроводностью в местах контакта. Исследование таких особенностей теплообмена в промышленных условиях затруднено, поэтому на помощь приходит математическое моделирование. Сравнение различных моделей нагрева металла в нагревательных печах [2, 3] позволяет классифицировать их на статистические [4, 5], аналитические [6] и численные [7 – 10], причем рассматривающие не только прямые, но и обратные задачи теплопроводности [6, 11]. Математические модели печных процессов также широко применяются для решения оптимизационных задач [11 – 15] и используют возможности современных CFD-комплексов [16, 17].
Целью данной работы является разработка математической модели нагрева сляба в печи с шагающими балками с учетом воздействия этих балок на процесс нагрева и применение ее для изучения температурного поля сляба.
Методы исследования
Разработанная модель представляет собой трехмерную нестационарную задачу теплопроводности в декартовой системе координат для расчетной области в форме параллелепипеда, без внутренних источников теплоты, с зависящими от температуры теплофизическими характеристиками и несимметричными граничными условиями третьего рода, имеющими кусочный характер на нижней поверхности расчетной области.
С учетом перечисленных допущений уравнение теплопроводности нелинейно и имеет вид:
| \(\begin{array}{c}\frac{{\partial T}}{{\partial t}} = \frac{1}{{{\rm{\rho }}c}}\left[ {\frac{\partial }{{\partial x}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{\rm{\lambda }}\frac{{\partial T}}{{\partial z}}} \right)} \right]{\rm{, }}\\\left\{ {{\rm{0}} < x < {{\rm{\delta }}_x},{\rm{0}} < y < {{\rm{\delta }}_y},{\rm{ 0}} < z < {{\rm{\delta }}_z}} \right\}\end{array}\). | (1) |
Начальное температурное поле однородно и выглядит как
| T(x, y, z) = Tн . | (2) |
При этом граничные условия могут быть записаны в виде:
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right)} \right|_{x = 0}} = \alpha _x^ \uparrow \left( {{T_{\rm{г}}} - {T_{x = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right)} \right|_{x = {\delta _x}}} = \alpha _x^ \downarrow \left( {{T_{\rm{г}}} - {T_{x = {\delta _x}}}} \right);\end{array}\); | (3) |
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right)} \right|_{y = 0}} = \alpha _y^ \uparrow (z)\left( {T_{\rm{г}}^ \uparrow (z) - {T_{y = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right)} \right|_{y = {\delta _y}}} = \alpha _y^ \downarrow \left( {{T_{\rm{г}}} - {T_{y = {\delta _y}}}} \right)\end{array}\); | (4) |
| \(\begin{array}{c} - {\left. {\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right)} \right|_{z = 0}} = \alpha _z^ \uparrow \left( {{T_{\rm{г}}} - {T_{z = 0}}} \right),\\{\left. {\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right)} \right|_{z = {\delta _z}}} = \alpha _z^ \downarrow \left( {{T_{\rm{г}}} - {T_{z = {\delta _z}}}} \right)\end{array}\). | (5) |
В выражениях (1) – (5), образующих замкнутую постановку дифференциальной задачи теплопроводности, использованы следующие обозначения: T(x, y, z, t) – температура заготовки, К; δx , δy , δz – размеры сляба по соответствующим координатным направлениям (ширина, толщина, длина), м; ρ – плотность материала сляба, кг/м3; с – удельная теплоемкость материала сляба, Дж/(кг·К); λ – коэффициент теплопроводности материала сляба, Вт/(м·К); \(\alpha_x^\uparrow\) и \(\alpha_x^\downarrow\) – коэффициенты теплоотдачи на задней и передней вертикальных поверхностях сляба соответственно, Вт/ (м2·К); \(\alpha_y^\uparrow\) и \(\alpha_y^\downarrow\) – коэффициенты теплоотдачи на нижней и верхней поверхностях сляба соответственно, Вт/(м2·К); \(\alpha_z^\uparrow\) и \(\alpha_z^\downarrow\) – коэффициенты теплоотдачи на левой и правой торцевых поверхностях сляба соответственно, Вт/(м2·К); Тг – температура греющей среды, К.
Уравнения задачи теплопроводности записаны в системе координат, связанной со слябом, поэтому вся специфика моделируемой печи может быть отражена в граничных условиях. Во-первых, для учета различия условий нагрева в разных технологических зонах печи коэффициенты теплоотдачи и температура греющей среды должны быть заданы как кусочная функция времени. Во-вторых, возможность задания этих характеристик различными для разных поверхностей сляба позволяет учесть геометрию печи. Так, например, если печь имеет монолитный под (что характерно для толкательных печей и печей с шагающим подом), то коэффициент \(\alpha_y^\uparrow\) может быть задан равным нулю. Таким образом, может быть формализовано условие адиабатности на нижней поверхности сляба. Для печей с шагающими балками граничные условия на верхней и нижней поверхностях сляба должны отражать различную интенсивность подвода теплоты в нижней и верхней частях рабочего пространства печи. Несмотря на наличие в обеих частях зон горения, в нижней части присутствует значительное экранирование поверхности сляба элементами механизма транспортировки. Кроме того, на нижней поверхности имеются зоны контакта с рейтерами подвижных и неподвижных балок, поэтому граничные условия должны задаваться различными для трех типов областей нижней поверхности:
– находящихся между балками (тип 0);
– периодически контактирующих с подвижными балками (тип 1);
– в основном контактирующих с неподвижными балками (тип 2).
Это означает, что \(\alpha _y^ \uparrow (z)\) и \(T_{\rm{г}}^ \uparrow (z)\), входящие в граничные условия на нижней поверхности сляба, являются кусочными функциями координаты вдоль сляба, помимо кусочного характера изменения во времени, как для остальных граничных условий. При этом должно быть учтено, что на разных этапах цикла шагания (т. е. перемещения сляба) различаются как условия контакта с различными балками, так и степень экранирования нижней поверхности сляба. В разработанной модели предложено описывать теплоотдачу на участке нижней поверхности сляба в момент его контакта с охлаждаемой балкой с помощью условных коэффициентов теплоотдачи \({\tilde \alpha _{\rm{н}}}\) и \({\tilde \alpha _{\rm{п}}}\), Вт/(м2·К). Теплоотдача происходит к среде с температурой \({\tilde T_{\rm{н}}}\) или \({\tilde T_{\rm{п}}}\), К, циркулирующей в системе охлаждения балок, где обычно применяют водяное или пароводяное охлаждение. Для пламенных печей (к которым относятся печи с шагающими балками) коэффициенты теплоотдачи учитывают не только конвективный, но и радиационный перенос (линеаризация граничных условий в форме (3) – (5) полезна для ускорения сходимости при последующем численном решении).
Цикл шагания состоит из отдельных этапов, названия которых и примерные значения продолжительностей позаимствованны из характеристик одной из печей ЛПЦ-2 ОАО «Северсталь». Пример характеристик работы механизма шагания представлен в табл. 1.
Таблица 1. Пример характеристик работы механизма шагания
|
Необходимо отметить, что информации, представленной в табл. 1, недостаточно для оценки времени контакта с балками. Требуется знание периода выдачи заготовок τ, с (минимальное значение которого равно суммарной продолжительности периода шагания, но на практике реальное значение обычно в несколько раз больше) и периода расположения слябов вдоль печи L, м (равного сумме ширины сляба и величины зазора между слябами). Тогда за период выдачи τ время контакта с подвижными балками составляет [7]:
| \({{\rm{\tau }}_{\rm{п}}} = \frac{L}{l}\left( {{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }} \right)\), | (6) |
а время контакта со стационарными балками вычисляется, как
| \({{\rm{\tau }}_{\rm{н}}} = {\rm{\tau }} - \frac{L}{l}\left( {{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }} \right)\). | (7) |
При моделировании процесса нагрева изменение граничных условий в соответствии с текущим этапом шагания представляется нецелесообразным, поскольку этот подход потребует очень маленьких расчетных шагов по времени (Δt ≤ 1 с). Поэтому целесообразно задавать граничные условия на участках, контактирующих с балками, как средневзвешенный результат с учетом доли времени контакта. При таком подходе устраняется зависимость от кратности продолжительностей этапов шагания расчетным шагам по времени. Тогда эффективный коэффициент теплоотдачи, который может быть задан в качестве граничного условия на участке нижней поверхности i-го типа, вычисляется по формуле
| \[\alpha _y^ \uparrow ({z_i}) = \left\{ {\begin{array}{*{20}{c}}{{\alpha ^ \uparrow },}\\{{\alpha ^ \uparrow }\left( {1 - \xi } \right) + \xi {{\tilde \alpha }_{\rm{п}}},}\\{{\alpha ^ \uparrow }\xi + {{\tilde \alpha }_{\rm{н}}}\left( {1 - \xi } \right),}\end{array}\begin{array}{*{20}{c}}{i = 0}\\{i = 1}\\{i = 2}\end{array}} \right.\], | (8) |
а эффективная температура среды, контактирующей с участком нижней поверхности i-го типа, по формулам
| \(T_{\rm{г}}^ \uparrow ({z_i}) = \large \left\{ \begin{array}{l}{T_{\rm{г}}},{\rm{ }}i = 0\\\frac{{{\rm{\xi }}{{{\rm{\tilde \alpha }}}_{\rm{п}}}{{\tilde T}_{\rm{п}}} + \left( {1 - {\rm{\xi }}} \right){{\rm{\alpha }}^ \uparrow }{T_{\rm{г}}}}}{{{\rm{\xi }}{{{\rm{\tilde \alpha }}}_{\rm{п}}} + \left( {1 - {\rm{\xi }}} \right){{\rm{\alpha }}^ \uparrow }}}{\rm{, }}i = 1\\\frac{{\left( {{\rm{1}} - {\rm{\xi }}} \right){{{\rm{\tilde \alpha }}}_{\rm{н}}}{{\tilde T}_{\rm{н}}} + {\rm{\xi }}{{\rm{\alpha }}^ \uparrow }{T_{\rm{г}}}}}{{\left( {{\rm{1}} - {\rm{\xi }}} \right){{{\rm{\tilde \alpha }}}_{\rm{н}}} + {\rm{\xi }}{{\rm{\alpha }}^ \uparrow }}}{\rm{, }}i = 2\end{array} \right.\), | (9) |
в которых вспомогательный коэффициент ξ характеризует долю времени контакта сляба с подвижными балками:
| \({\rm{\xi }} = \frac{{{{\rm{\tau }}_{\rm{п}}}}}{{\rm{\tau }}} = \frac{L}{l}\frac{{{{\rm{\tau }}_ \uparrow } + {{\rm{\tau }}_ \to } + {{\rm{\tau }}_ \downarrow }}}{{\rm{\tau }}}\). | (10) |
Нелинейная задача (1) – (5) не имеет аналитического решения, поэтому решать ее приходится методом конечных разностей (методом баланса) [7, 18, 19].
Этот метод предполагает введение дискретного времени tk = kΔt (k = 1, 2, ...) с постоянным шагом Δt и дискретных координат xi = iΔx (i = 0, 1, 2, .., nx ), yj = jΔy (j = 0, 1, 2, .., ny ), zl = lΔz (l = 0, 1, 2, .., nz ), которые для данной простой геометрии также изменяются с постоянными шагами Δx, Δy и Δz. Значения nx , ny и nz называют количеством разбиений заготовки вдоль каждого из координатных направлений.
В результате вся расчетная область разбивается на элементарные объемы, количество которых равно (nx + 1)(ny + 1)(nz + 1). Каждый из этих объемов содержит один узел пространственной сетки, которая задается трехиндексной нумерацией (i, j, l). На каждом шаге по времени для каждого элементарного объема записываются уравнения элементарного теплового баланса, образующие квазилинейную систему уравнений относительно узловых значений температуры в конце шага по времени, решение которой общими методами нецелесообразно [19, 20].
Результаты исследования
Программная реализация разработанной математической модели осуществлена в визуальной среде разработки Builder C++ версии 6.0. В расчетной программе предлагается выбор одного из трех алгоритмов решения системы разностных уравнений:
– метод расщепления (применим только для линейных задач);
– метод простой итерации (не требует больших затрат памяти, но медленно сходится);
– послойный метод (прямое решение для распространения теплоты по толщине сляба с итерационным уточнением ее распространения по длине и ширине).
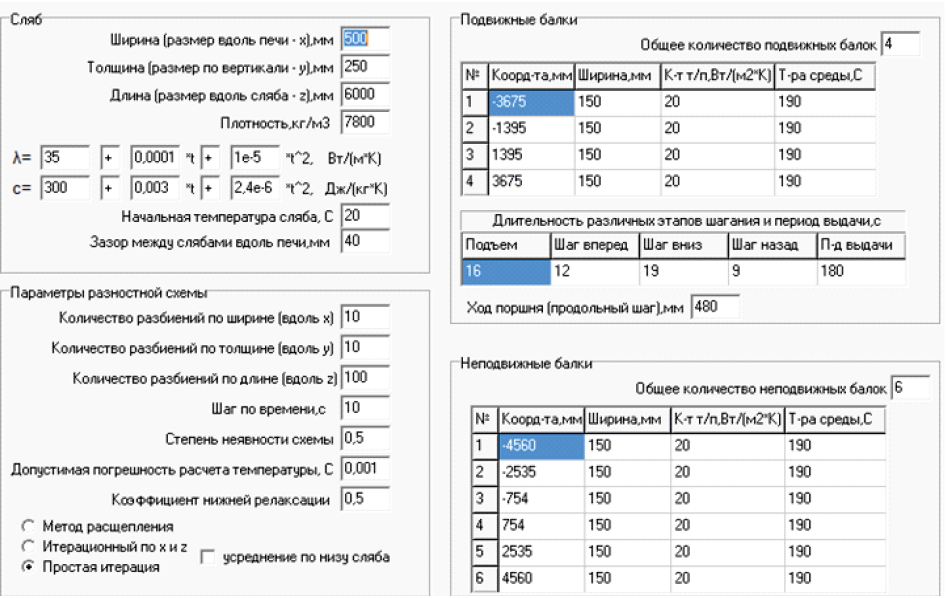
Знание величин \({\tilde \alpha _{\rm{н}}}\), \({\tilde \alpha _{\rm{п}}}\), \({\tilde T_{\rm{н}}}\), \({\tilde T_{\rm{п}}}\) возможно только на основе экспериментальных данных и модели теплообмена между нижней поверхностью сляба и элементами системы его транспортировки. В рамках настоящей программной реализации они являются внешними исходными данными. На этом этапе работы предложено учесть только экранирующий эффект элементов системы транспортировки, задав для величин \({\tilde \alpha _{\rm{н}}}\) и \({\tilde \alpha _{\rm{п}}}\) нулевые значения. На рис. 1 представлены исходные данные, при которых проведены расчеты, а в табл. 2 – режимные характеристики, отражающие особенности нагрева сляба в пятизонной печи.
Рис. 1. Снимок экрана программы с исходными данными для моделирования |
Таблица 2. Параметры режима нагрева при моделировании
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
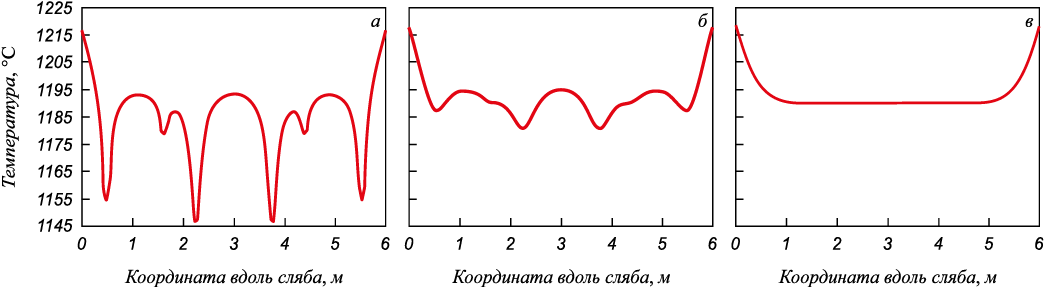
В процессе расчетов контролировалось соблюдение теплового баланса для сляба как на каждом шаге по времени, так и глобально для всего расчета (расхождение не более 0,001). На рис. 2 представлены конечные температурные профили для нижней (а) и верхней (б) поверхностей сляба (изменение температуры вдоль продольной оси поверхности) с размерами 250×500×6000 мм, нагреваемого в печи, оснащенной четырьмя неподвижными и двумя подвижными балками. На рис. 2, в для сравнения показан температурный профиль вдоль оси нижней поверхности, нагреваемой при однородных граничных условиях, соответствующих тем же средним значениям.
Рис. 2. Температурный профиль вдоль оси нижней (а) и верхней (б) поверхностей сляба |
Обсуждение результатов исследования
Полученные результаты демонстрируют, что вблизи торцов сляба температура на оси верхней и нижней его поверхностей повышается примерно на 20 – 25 °C независимо от типа граничных условий, что вызвано влиянием подачи теплоты к торцам сляба. При этом, в случае однородных граничных условий на нижней поверхности, температурный профиль в остальной части оси нижней поверхности сляба получается практически однородным (рис. 2, в), тогда как при кусочном задании граничных условий неоднородность температурного поля в этой части достигает 48 °С (рис. 2, а). Неоднородность температурного поля проявляется и на верхней грани сляба, хотя и существенно менее выражена в количественном плане (около 15 °С вдали от концов сляба, рис. 2, б). Можно также заметить, что для неподвижных балок «пятно» воздействия глубже и шире, чем для подвижных балок (рис. 2, а). Это обусловлено тем, что время контакта участков нижней поверхности сляба с неподвижными балками больше, чем с подвижными.
Разработанная программа расчета и визуализации результатов может быть использована для изучения температурного поля сляба при различных режимах его нагрева в случае наличия экспериментальной информации, позволяющей уточнить настроечные параметры модели \({\tilde \alpha _{\rm{н}}}\), \({\tilde \alpha _{\rm{п}}}\), \({\tilde T_{\rm{н}}}\), \({\tilde T_{\rm{п}}}\). Результаты, полученные в данной работе при учете только экранирующего воздействия балок, следует рассматривать как оценку снизу для неоднородности температурного поля сляба.
Выводы
Разработана и программно реализована математическая модель нагрева сляба в печи с шагающими балками, учитывающая воздействие этих балок на нижнюю поверхность сляба. Модель представляет собой трехмерную нестационарную задачу теплопроводности с граничными условиями третьего рода, имеющими кусочный характер на нижней поверхности сляба.
Для печи, оснащенной четырьмя неподвижными и двумя подвижными балками, смоделирован нагрев сляба 250×500×6000 мм по штатному режиму при учете только экранирующего воздействия балок на нижнюю поверхность сляба. Неоднородность температуры по нижней поверхности сляба вдали от торцов составила около 48 °С, а по верхней поверхности сляба – около 15 °С.
Список литературы
1. Гусовский В.Л., Лифшиц А.Е. Методики расчета нагревательных и термических печей: Учебно-справочное издание. М.: Теплотехник; 2004: 400.
2. Тимошпольский В.И., Трусова И.А., Менделеев Д.В., Ратников П.Э. Анализ методов математического моделирования процессов теплообмена в промышленных печах для нагрева металла. Литье и металлургия. 2012; 2(65): 102–107.
3. Singh V.K., Talukdar P. Comparisons of different heat transfer models of a walking beam type reheat furnace. International Communications in Heat and Mass Transfer. 2013; 47: 20–26. https://doi.org/10.1016/j.icheatmasstransfer.2013.06.004
4. Беленький А.М., Богатова М.Ж., Чибизова С.И. Статическое моделирование нагрева металла в печах с шагающими балками. Черные металлы. 2021; 8: 32–37. https://doi.org/10.17580/chm.2021.08.06
5. Богатова М.Ж., Чибизова С.И. Статистическое моделирование температурных режимов работы нагревательных печей листовых станов горячей прокатки. Известия вузов. Черная металлургия. 2021; 64(5): 374–381. https://doi.org/10.17073/0368-0797-2021-5-374-381
6. Левицкий И.А. Линейная задача теплопроводности для тел правильной формы при граничных условиях третьего рода. Черные металлы. 2019; 10: 67–72.
7. Абдукодиров И.Б. Математическая модель нагрева сляба в печи с шагающими балками: дис. магистра: 22.04.02. Москва; 2020: 68.
8. Han S.H., Chang D., Kim C.Y. A numerical analysis of slab heating characteristics in a walking beam type reheating furnace. International Journal of Heat and Mass Transfer. 2010; 53(19-20): 3855–3861. https://doi.org/10.1016/j.ijheatmasstransfer.2010.05.002
9. Курносов В.В., Левицкий И.А., Прибытков И.А. Исследование нагрева массивных заготовок с различными скоростями в печах периодического действия. Известия вузов. Черная металлургия. 2012; 55(9): 27–31. https://doi.org/10.17073/0368-0797-2012-9-27-31
10. Landfahrer M., Schluck C. Numerical and experimental investigation of scale formation on steel tubes in a real-size reheating furnace. International Journal of Heat and Mass Transfer. 2019; 129: 460–467. https://doi.org/10.1016/j.ijheatmasstransfer.2018.09.110
11. Курносов В.В., Левицкий И.А. Математическое моделирование нагрева заготовок с переменными теплофизическими характеристиками и теплового режима, соответствующего заданному графику нагрева. Известия вузов. Черная металлургия. 2012; 55(7): 19–22. https://doi.org/10.17073/0368-0797-2012-7-19-22
12. Jang J.-Y., Huang J.-B. Optimization of a slab heating pattern for minimum energy consumption in a walking-beam type reheating furnace. Applied Thermal Engineering. 2015; 85: 313–321. https://doi.org/10.1016/J.APPLTHERMALENG.2015.04.029
13. Tang G., Wu B., Bai D., Wang Y., Bodnar R., Zhou C.Q. Modeling of the slab heating process in a walking beam reheating furnace for process optimization. International Journal of Heat and Mass Transfer. 2017; 113: 1142–1151. https://doi.org/10.1016/j.ijheatmasstransfer.2017.06.026
14. Ding J.G., Kong L.P., Guo J.H., Song M.X., Jiao Z.J. Multi-objective optimization of slab heating process in walking beam reheating furnace based on particle swarm optimization algorithm. Steel Research International. 2021; 92(3): 2000382. https://doi.org/10.1002/srin.202000382
15. Tang L., Liu J., Rong A., Yang Z. An effective heuristic algorithm to minimise stack shuffles in selecting steel slabs from the slab yard for heating and rolling. Journal of the Operational Research Society. 2001; 52(10): 1091–1097. https://doi.org/10.1057/palgrave.jors.2601143
16. Tang G., Wu B., Wang Y., Bodnar R., Zhou C. CFD modeling and validation of a dynamic slab heating process in an industrial walking beam reheating furnace. Applied Thermal Engineering. 2018; 132: 779–789. https://doi.org/10.1016/j.applthermaleng.2018.01.017
17. Mayr B., Prieler R., Demuth M., Moderer L., Hochenauer C. CFD analysis of a pusher type reheating furnace and the billet heating characteristic. Applied Thermal Engineering. 2017; 115: 986–994. https://doi.org/10.1016/j.applthermaleng.2017.01.028
18. Арутюнов В.А., Бухмиров В.В., Крупенников С.А. Математическое моделирование тепловой работы промышленных печей. М.: Металлургия; 1990: 239.
19. Кудинов В.А., Кудинов И.В. Методы решения параболических и гиперболических уравнений теплопроводности. М.: Книжный дом «Либроком»; 2012: 280.
20. Mathews J.H. Computer derivations of numerical differentiation formulae. International Journal of Mathematics Education in Science and Technology. 2003; 34(2): 280–287. https://doi.org/10.1080/0020739031000158317
Об авторах
И. Б. Абдукодиров
Дочернее предприятие «Литейно-механический завод» Унитарного предприятия «O'ztemiryo'lmashta'mir»
Россия
Россия
Илхомжон Бахтиерович Абдукодиров, заместитель начальника участка заготовки и сортировки металла
Республика Узбекистан, 100213, Ташкент, ул. Х. Байкаро, 41
А. В. Варгин
Национальный исследовательский технологический университет «МИСИС»
Россия
Россия
Александр Вячеславович Варгин, аспирант кафедры энергоэффективных и ресурсосберегающих промышленных технологий
Россия, 119049, Москва, Ленинский пр., 4
И. А. Левицкий
Национальный исследовательский технологический университет «МИСИС»
Россия
Россия
Игорь Анисимович Левицкий, к.т.н., доцент кафедры энергоэффективных и ресурсосберегающих промышленных технологий
Россия, 119049, Москва, Ленинский пр., 4
Рецензия
Для цитирования:
Абдукодиров И.Б., Варгин А.В., Левицкий И.А. Математическая модель нагрева сляба в печи с шагающими балками. Известия высших учебных заведений. Черная Металлургия. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
For citation:
Abdukodirov I.B., Vargin A.V., Levitskii I.A. Simulation of slab heating in a walking beam furnace. Izvestiya. Ferrous Metallurgy. 2023;66(1):112-118. https://doi.org/10.17073/0368-0797-2023-1-112-118
Просмотров:
858
Послать статью по эл. почте 