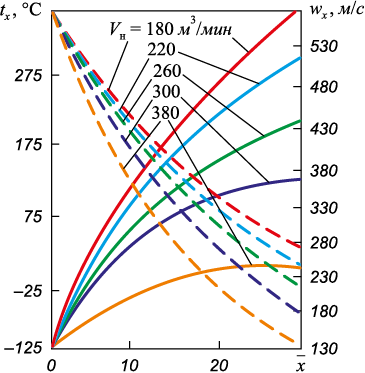Перейти к:
Моделирование термогазодинамических параметров нейтральных газовых струй при распространении в полости конвертера
https://doi.org/10.17073/0368-0797-2022-12-843-850
Аннотация
С учетом волновой структуры течения сверхзвуковой струи, истекающей в рабочее пространство конвертера после выпуска металла, рассмотрены особенности и характеристики процессов распространения нейтральных газовых струй на газодинамическом участке до начала взаимодействия со шлаковым расплавом, в дальнейшем раздуваемым для нанесения огнеупорного гарнисажа на футеровку агрегата. Рассматривается модель расчета присоединенной массы окружающего газа, находящегося в рабочем пространстве конвертера. При постановке задачи учитываются известные данные по газодинамике при формировании и течении струи, которые оказывают влияние на эффективность турбулентного переноса в пограничном слое. В основе схемы расчета лежит гипотеза существования начальной границы, через которую в газовую струю проникает химически активный газ из окружающей среды, а форма предельной границы предполагается цилиндрической с радиусом, равным максимальному радиусу первой бочки нерасчетной струи. Численные расчеты позволяют определить среднемассовую скорость и температуру в произвольном сечении сверхзвуковой нерасчетной струи до внедрения ее в шлаковый расплав. Установлено влияние относительной температуры θ, температуры азота перед соплом Т0 при распространении струи в полости конвертера и расхода азота через сопла V0 на величину присоединенной массы q, осредненные значения скорости Wх и температуры Tх в произвольном сечении x сверхзвуковой нерасчетной струи на газодинамическом участке. Полученная информация может быть использована при разработке систем газопорошковой продувки в агрегатах и сталеразливочных ковшах, систем торкретирования и подачи нейтральных газовых струй при замещении кислородных потоков по ходу продувки и использовании двухярусных фурм.
Ключевые слова
Для цитирования:
Протопопов Е.В., Думова Л.В., Чернышева Н.А., Ноздрин И.В., Сафонов С.О. Моделирование термогазодинамических параметров нейтральных газовых струй при распространении в полости конвертера. Известия высших учебных заведений. Черная Металлургия. 2022;65(12):843-850. https://doi.org/10.17073/0368-0797-2022-12-843-850
For citation:
Protopopov E.V., Dumova L.V., Nozdrin I.V., Chernysheva N.A., Safonov S.O. Modeling of thermogasodynamic parameters of neutral gas jets when spreading in converter cavity. Izvestiya. Ferrous Metallurgy. 2022;65(12):843-850. (In Russ.) https://doi.org/10.17073/0368-0797-2022-12-843-850
Введение
В настоящее время характерной особенностью работы отечественных [1 – 3] и зарубежных [4 – 7] конвертерных цехов является постоянное использование технологии «горячих» ремонтов футеровки путем нанесения шлакового гарнисажа, получаемого при раздувке конечного шлака нейтральными газовыми струями. При этом, как правило, к основным мероприятиям повышения эффективности такой технологии относят совершенствование подготовки шлакового расплава [8 – 12] и конструкции гарнисажных дутьевых устройств [1 – 3, 7] при формировании структуры и параметров нейтральных газовых струй с обеспечением максимально возможной подводимой к шлаку энергии [13 – 16].
В соответствии с современными представлениями [17 – 20] сверхзвуковая газовая струя с умеренной нерасчетностью характеризуется развитой системой скачков уплотнения и ударных волн различной интенсивности, генерирующих к тому же и акустические волны. В то же время из-за диссипативных процессов на участках скачков давления при чередующихся во времени и пространстве разрежениях и сжатиях, а также присоединения газа из рабочего пространства конвертера, часть динамической энергии газовых струй теряется. При этом происходит искажение контуров, увеличение угла раскрытия, изменение характера распределения скоростей в сечении струи. В работах Е.А. Капустина и сотрудников, например, в работе [13], практически впервые выполнены экспериментальные исследования по определению величины присоединенной к струе массы высокотемпературного химически активного газа из рабочего пространства конвертера и оценки развития процессов в пограничном слое струи.
Целью настоящего исследования являются анализ, исследование и установление влияния относительной температуры \(\theta = \frac{{{T_{\rm{г}}}}}{{{T_0}}}\), температуры азота перед соплом t0 и при распространении в полости конвертера tг , расхода азота через сопло Vн на величину присоединенной массы g, осредненные значения скорости Wх и температуры tх в произвольном сечении \(\bar x\) сверхзвуковой нерасчетной струи на газодинамическом участке до начала взаимодействия со шлаковым расплавом в конвертере.
Принятые обозначения
В настоящей работе приняты следующие обозначения: m – массовый расход; \(g = \frac{{{m_{\rm{}}}}}{{{m_t}}}\) – присоединенная масса; \(\bar g = \frac{{{m_{\rm{1}}}}}{{{m_1} + {m_{\rm{г}}}}}\) и \({\bar g_{\rm{г}}} = \frac{{{m_{\rm{г}}}}}{{{m_1} + {m_{\rm{г}}}}}\) – концентрация истекающего из сопла азота и газа в полости конвертера; Vн – объемный расход; a и aкр – местная скорость звука и критическая скорость; T – термодинамическая температура; p – абсолютное давление; \(\theta = \frac{{{T_{\rm{г}}}}}{{{T_0}}}\) – относительная температура; ρ – плотность; w – средняя скорость в определенном сечении струи; \(M = \frac{w}{a}\) – число Маха; \(\lambda = \frac{w}{{{a_{{\rm{кр}}}}}}\) – приведенная скорость; \(\frac{{{T_1}}}{{{T_0}}} = \tau (\lambda )\) – газодинамическая функция температуры; \(n = \frac{p}{{{p_{\rm{г}}}}}\) – степень нерасчетности истекающей струи; \(k = \frac{{{c_p}}}{{{c_v}}}\) – показатель адиабаты; \(C = \sqrt {1 - {{\left( {\frac{{k - 1}}{2}{M^2}} \right)}^{ - 1}}} \) – число Крокко; β – коэффициент количества движения; α – коэффициент кинетической энергии; F – площадь сечения; Υ0 – начальный угол раскрытия по границе сверхзвуковой струи; \(\bar x\) – расстояние, пройденное струей в диаметрах критического сечения сопла dкр .
Индексы «0» и «1» обозначают параметры перед соплом и в выходном сечении сопла; «кр» – в критическом сечении сопла; «х» – в произвольном сечении истекающей газовой струи; «i» – на поверхности струи; «г» – газа в полости конвертера»; индекс «н» показывает, что процесс идет в нормальных физических условиях.
Расчетная модель
При постановке задачи учтены данные по газодинамике при формировании и течении струй, оказывающих влияние на эффективность турбулентного переноса в пограничном слое при взаимодействии с газом в полости конвертера.
Схема расчета основана на гипотезе существования идеальной границы, через которую в нейтральную газовую струю проникает химически активный газ из окружающей среды. Эта граница является условной, так как она существовала бы только в случае, если бы газовые струи и газ окружающего пространства были совершенными. Однако такая формулировка удобна как пространственный базис, каким в теории пограничного слоя является твердая стенка, относительно которой рассматривается вязкое течение при смешении газов. В такой постановке допущение состоит в том, что форма предельной границы струи предполагается цилиндрической с радиусом, равным максимальному радиусу первой бочки нерасчетной струи [21 – 25]. Тогда угол раскрытия сверхзвуковой струи при выходе из сопла можно определить по выражению
| Yo ≈ ω(M1 ) – ω(Mi ) + α, | (1) |
где функция
| \[\omega {\rm{(}}M{\rm{) = }}\sqrt {\frac{{k + 1}}{{k - 1}}} arctg\sqrt {\frac{{k - 1}}{{k + 1}}{\rm{(}}{M^2} - 1{\rm{)}}} - arctg\sqrt {{M^2} - 1} .\] | (2) |
Максимальный радиус первой бочки нерасчетной струи составляет \({\bar r_{{\rm{max}}}} = \left( {1 + \frac{{{\Upsilon _{\rm{o}}}}}{\psi }} \right)\) (где Yo – функция Прандтля-Майера), а ψ можно определить как
| \[\psi = \frac{1}{{\sqrt {M_1^2 - 1} }}\frac{{q({M_i})}}{{q({M_1})}}.\] | (3) |
Газодинамическую функцию расхода газа, выраженную через число Маха Мг , можно представить в виде
| \[q({M_1}) = {\left( {\frac{{k + 1}}{2}} \right)^{\frac{{k + 1}}{{2(k - 1)}}}}{M_1}{\left( {1 + \frac{{k - 1}}{2}M_1^2} \right)^{\frac{{k + 1}}{{2(k - 1)}}}}.\] | (4) |
Тогда присоединенную к струе массу можно рассчитать по выражению
| \[g = \frac{{{m_{\rm{г}}}}}{{{m_1}}},\] | (5) |
где m1 = ρ1w1 F1 – расход газа через сопло.
При постановке задачи присоединенную массу g дополнительно рассчитывали по соотношению
| \[g = \frac{{2{{\bar r}_{{\rm{max}}}}{\rm{ }}\bar x}}{{D\sigma }}{C_i}{\left( {1 - C_i^2} \right)^{1/2}}\left( {{I_{1R}} - {I_{2R}}} \right),\] | (6) |
где \(D = \sqrt {\frac{{k - 1}}{2}} {M_1}{n^{\frac{{k + 1}}{{2k}}}}\) – параметр, связывающий число Маха М1 и степень нерасчетности струи n, определенную для условий выходного сечения сопла; σ = 12 + 2,58Мi – параметр подобия, характеризующий степень турбулентности струи; \({I_{1R}} = \int\limits_{ - \propto }^{{\eta _R}} {\frac{{\varphi d\eta }}{{1 - {\varphi ^2}C_i^2}}} ,{\rm{ }}{I_{2R}} = \int\limits_{ - \propto }^{{\eta _R}} {\frac{{{\varphi ^2}d\eta }}{{1 - {\varphi ^2}C_i^2}}} {\rm{ }}\) – интегралы (при истечении холодного газа в затопленное пространство θ = 1 и значения определяются графически [25]); η – безразмерная переменная в зоне смешения; R – индекс, относящийся к зоне смешения.
Степень нерасчетности струи также можно выразить через число Маха на срезе сопла M1 и на внешней границе струи Мi
| \[n = {\left( {\frac{{1 + \frac{{k - 1}}{2}M_i^2}}{{1 + \frac{{k - 1}}{2}M_1^2}}} \right)^{\frac{k}{{k - 1}}}}.\] | (7) |
При разработке модели более подробные преобразования, связанные с выражениями (5) и (6), выполнены в соответствии с работой [13].
Рассмотрим движение сверхзвуковой нерасчетной струи нейтрального газа на начальном участке от среза сопла до условного сечения х, находящегося, например, на уровне вхождения струи в шлаковый расплав. Длину так называемого газодинамического участка \(\bar x\) при истечении струи в условно «холодный» газ можно оценить, например, по результатам работ [21, 25]. При этом следует иметь в виду, что при истечении в высокотемпературное изобарное пространство, в сравнении с «холодным», длина сверхзвукового потока будет возрастать, а значит и расстояние газодинамического участка возрастает в зависимости от температуры окружающего газа ориентировочно в 1,3 – 1,7 раза [12 – 14]. Для этого участка запишем закон постоянства количества движения
| \[{F_1}({p_1} - {p_{\rm{г}}}) + \beta {\rho _1}w_1^2{F_1} = \int {\rho {w^2}dF + \int {(p - {p_{\rm{г}}})} } dF.\] | (8) |
Коэффициенты, характеризующие неравномерность распределения количества движения β и кинетической энергии α по сечению сверхзвуковой струи, можно определить как
| \[\begin{array}{l}\beta = \frac{{\int_F^{} {{w^2}dF} }}{{w_{{\rm{кр}}}^{\rm{2}}F}}{\rm{;}}\\\alpha = \frac{{\int_F^{} {{w^3}dF} }}{{w_{{\rm{кр}}}^{\rm{3}}F}}.\end{array}\] | (9) |
После интегрирования правой части уравнения (8) можно записать
| \[{F_1}({p_1} - {p_{\rm{г}}}) + \beta {\rho _1}w_1^2{F_1} = {\rho _x}w_x^2{F_x} + ({p_x} - {p_{\rm{г}}}){F_x}.\] | (10) |
С учетом уравнения (10) среднемассовую скорость струи на расстоянии х от среза сопла в соответствующем сечении, где статическое давление рх уравнивается с атмосферным р1 , рассчитывали по выражению
| \[{w_x} = \left[ {\frac{{{p_E}(n - 1)}}{{{\rho _1}{w_1}}} + \beta {w_1}} \right]\frac{1}{{(1 + g)\beta }},\] | (11) |
где w1 = λ1aкр – скорость истечения из сопла.
Приведенную скорость λ1 находили, используя газодинамическую функцию расхода \(q({\lambda _1}) = \frac{{{F_{{\rm{кр}}}}}}{{{F_1}}},\) которая известна, так как диаметры dкр и d1 определены конструкцией дутьевого устройства. При этом принимали, что рг = 0,1 МПа.
Для нахождения среднемассовой температуры tx решали уравнение теплового баланса для участка струи после выхода из сопла до определенного сечения х (излучением пренебрегали):
| \[\begin{array}{c}{m_1}{c_{p{\rm{г}}}}{T_0} + {m_1}{c_{p{\rm{г}}}}{T_{\rm{г}}} = \\ = ({m_1} + {m_{\rm{г}}}){c_{px}}{T_x} + \frac{{\alpha ({m_1} + {m_{\rm{г}}})w_x^2}}{{2000}}.\end{array}\] | (12) |
В соответствии с зависимостью (12) температуру Тх струи в сечении х представляли в виде
| \[{T_x} = {T_0}\bar g\frac{{{c_{p0}}}}{{{c_{px}}}} + {T_{\rm{г}}}{\bar g_{\rm{г}}}\frac{{{c_{p{\rm{г}}}}}}{{{c_{px}}}} - \frac{{\alpha w_x^2}}{{2000{c_{px}}}}.\] | (13) |
Таким образом, в соответствии с постановкой задачи и принятой моделью по аналогии с работой [19] в дальнейшем решали систему, состоящую из 45 алгебраических уравнений, а также численно рассчитывали интегралы I1р и I2р в зависимости от числа Крокко.
Исходные данные
При выполнении расчетов для условий эксплуатации 350 т конвертеров АО «ЕВРАЗ Западно-Сибирский металлургический комбинат» использовали характеристики и параметры применяемого дутьевого устройства. Температуру азота на входе в сопло t0 варьировали в пределах 25 – 600 °C, а температуру газа tг в полости конвертера в условиях отсутствия металла перед раздувкой шлака – в интервале 300 – 1000 °C. Теплоемкость азота ср в полости конвертера принимали равной 1,25 кДж/(кг·К). В случае расчетного режима истечения при n = 1 расход азота через одно сопло V составляет примерно 200 м3/мин.
Количество сопел в головке фурмы – 4. Диаметр сопла в критическом сечении dкр составляет 54 мм, во входном d0 и выходном d1 сечениях – 65 и 71 мм. Коэффициент количества движения 1,04, коэффициент кинетической энергии 1,3.
Результаты расчета и их анализ
Присоединенную массу g рассчитывали по уравнению (6).
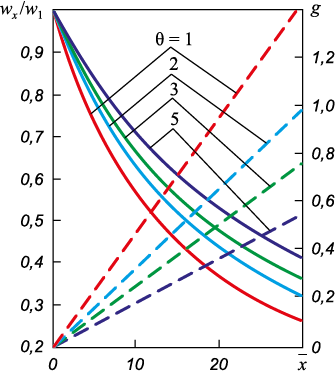
На рис. 1 показано влияние относительной температуры θ на изменение относительной скорости wх /w1 струи газа и присоединенной массы g по длине струи \(\bar x\) при t0 = 30 °C, Vн = 200 м3/мин, tг = 30 – 1500 °C. Установлено, что чем больше относительная температура θ (больше tг ), тем меньше масса газа, присоединяемого из полости конвертера. Так, на расстоянии \(\bar x\) = 20 при θ = 1 присоединенная масса g составляет 0,98, а при θ = 5 – только 0,35.
Рис. 1. Влияние относительной температуры θ на изменение относительной скорости wх /w1 |
Отмеченная особенность объясняется тем физически бесспорным фактом, что при увеличении значения θ плотность эжектируемой среды падает, снижается и масса подсасываемого присоединенного газа.
Как видно (рис. 1), по мере удаления от среза сопла отношение скоростей wх /w1 снижается при любом значении θ. Характерно, что чем больше значение θ, тем более высокотемпературным будет окружающий газ, тем меньше присоединенная масса g, и, по этой причине, отношение скоростей wх /w1 увеличивается. Например, при θ = 1 и \(\bar x\) = 30 относительная скорость wх /w1 составляет 0,28, а при повышении θ до 5 значение wх /w1 уже составляет 0,38.
Анализ результатов расчета показывает, что масса эжектируемого газа по мере удаления от сопла по оси струи будет нарастать практически линейно. В приложении к конвертерному процессу это будет означать, что чем выше высота расположения фурмы относительно уровня жидкой ванны, тем газовая струя в месте встречи с расплавом будет более насыщена (разбавлена) окружающим газом [19, 25]. И, соответственно, наоборот. Накопленный экспериментальный и производственный опыт проведения операции нанесения шлакового гарнисажа показывает [1 – 3, 25], что наилучшие результаты по разбрызгиванию шлака достигаются при расположении фурмы в положении, максимально приближенном к шлаковому расплаву, то есть газодинамический участок по длине будет незначительным и эжекция в струю окружающего газа минимальной.
Hecколькo неожиданной является полученная зависимость величины присоединенной массы g от температуры нагрева азота t0 , например, при использовании газоохлаждаемых (азотом) гарнисажных фурм. На рис. 2 представлены зависимости отношения скоростей wх /w1 и присоединенной массы g от температуры азота на входе в сопло t0 при различном удалении \(\bar x\) от среза сопла при t0 = 30 °С, Vн = 200 м3/мин, tг = 30 – 1500 °С.
Рис. 2. Зависимости отношения скоростей wх /w1 ( |
Расчетные данные показывают, что при удалении от среза сопла при любом значении t0 присоединенная масса увеличивается. C повышением температуры t0 присоединенная масса, казалось бы, должна расти. Однако, с увеличением степени нагрева азота перед соплом при m = const и появлением дополнительного теплового сопротивления давление p0 также возрастает, что в конечном счете приводит к снижению присоединенной к струе массы. Например, при повышении температуры азота на входе в сопло с 30 до 600 °С при распространении струи на расстоянии 20 калибров присоединенная масса уменьшается с 0,32 до 0,23. При этом относительная скорость wх /w1 возрастает с 0,54 до 0,58.
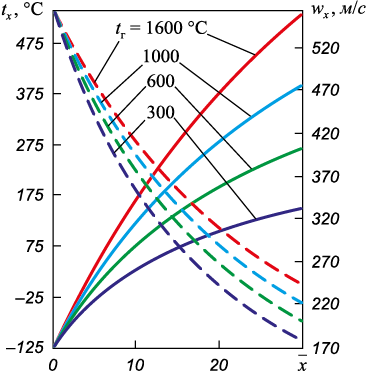
На рис. 3 приведены зависимости температуры tx и скорости wx от температуры газа в полости конвертера tг на различном удалении \(\bar x\) от среза сопла при t0 = 30 °С, Vн = 200 м3/мин, tг = 30 – 1500 °С. При увеличении tг температура tх возрастает, причем весьма существенно. Так, например, если tх увеличивается с 600 до 1000 °С, то на расстоянии 20 калибров температура tг возрастает со 170 до 270 °С. Скорость струи wx с увеличением tг повышается, так как струя попадает в более высокотемпературное пространство, а плотность окружающей среды снижается и при тех же условиях газовая струя, не встречая значительного сопротивления, ускоряется с 210 до 310 м/с.
Рис. 3. Зависимости температуры tx ( |
Расход газа Vн увеличивается за счет повышения давления и по этой причине присоединенная масса в одном и том же сечении струи будет меньше (рис. 4). Тогда температура tx также будет снижаться, а скорость wx с увеличением расхода Vн возрастать. Например, на расстоянии 20 калибров и при увеличении расхода газа Vн со 180 до 360 м3/мин температура газа будет возрастать с 270 до 542 °С, а скорость – с 200 до 330 м/с.
Рис. 4. Изменение температуры tx ( |
Проверка адекватности модели
Совершенно очевидно, что подтвердить численные расчеты проведением прямых промышленных экспериментов на конвертерах емкостью 350 т не представляется возможным, поэтому допустимо использование метода тестовой проверки достоверности полученной модели. Так, например, подтверждается, что:
– на срезе сопла (\(\bar x\) = 0) присоединения окружающего газа нет (g = 0) и wх /w1 = 1 при любых значениях θ и t0 (см. рис. 1, 2);
– если \(\bar x\) = 0, то wх = w1 = λ1aкр , а tх = t1 = –120 °С, что также следует из выражения Т1 = Т0τ(λ) (см. рис. 3);
– если \(\bar x\) = 0 и tх = t1 = –120 °С, то wх = w1 = λ1aкр ;
– чем большее расстояние от среза сопла прошла газовая струя, тем больше независимо от t0 , tг , Vн cкорость струи wx снижается, а tх возрастает, что соответствует физической картине присоединения горячего газа окружающей среды к струе любой структуры.
Выводы
Проведено численное моделирование параметров струи нейтрального газа при распространении в полости конвертера в условиях отсутствия металла на участке до начала взаимодействия со шлаковым расплавом.
Список литературы
1. Мокринский А.В., Лаврик А.Н., Соколов В.В., Протопопов Е.В., Чернятевич А.Г. Перспективные направления продления срока службы футеровки конвертеров // Сталь. 2004. № 5. С. 40–44.
2. Протопопов Е.В., Галиуллин Т.Р., Чернятевич А.Г., Соколов В.В. Разработка конструкции гарнисажных фурм и технологии газопорошкового ошлакования 350-т конвертеров Западно-Сибирского металлургического комбината // Черная металлургия. Бюллетень научно-технической и экономической информации. 2009. № 9. С. 34–39.
3. Нугуманов Р.Ф., Протопопов Е.В., Галиуллин Т.Р., Чернятевич А.Г., Чубина Е.А. Новое направление в совершенствовании технологии нанесения шлакового гарнисажа на футеровку конвертера // Известия вузов. Черная металлургия. 2006. № 12. С. 7–12.
4. Sian C., Wenyan Y., Conglie Z. Slag splashing for Bao Steel′s 300 metric ton BOF and crystallographic structure of its slag // Iron and Steelmaker. 2000. Vol. 27. No. 7. P. 39–41.
5. Lin L., Xiaoyan P., Fei G., Hewei D. Improvement and maintenance of MgO-C bottom-blowing tuyere in BOF converter for prolonging service life. In: Proceedings of the Unified Int. Tech. Conf. on Refractories. Chapter 124. UNITECR. 2013. P. 721–725. https://doi.org/10.1002/9781118837009.ch124
6. Sarkar S., Pal Т.К., Ghosh N.K., Garai S.K., Chintaiah P., Kujur M.K., Mishra A.N., Datta P.K. Enhancement of BOF productivity through modification of hot metal transfer ladle lining at Durgapur steel plant // SEAISI Quarterly (South East Asia Iron and Steel Institute). 2009. Vol. 38. No. 1. P. 39–42.
7. Zhaslan R.K., Zhautikov B.A., Romanov V.I., Aikeyeva A.A., Yerzhanov A.S. Improvement of methods for semi-finished carbon product tapping from the basic oxygen furnace (BOF) // Metalurgija. 2022. Vol. 61. No. 1. P. 203–205.
8. Высокомагнезиальные флюсы для сталеплавильного производства / К.Н. Демидов, Т.В. Борисова, А.П. Возчиков и др. Москва: Завод брикетированных материалов, 2013. 280 с.
9. Barron M.A., Hilerio I. Numerical analysis of slag splashing in a steelmaking converter // Computer Technology and Application. 2011. Vol. 2. No. 9. P. 828–834.
10. Slovikovskii V.V., Gulyaeva A.V. Creation of high-efficiency promising refractory materials and constructions for the lining of metallurgical units // Refractories and Industrial Ceramics. 2018. Vol. 58. No. 5. P. 475–480. https://doi.org/10.1007/s11148-018-0130-7
11. Cong I.G., Wei Y., Zhang Y., Peng F. Practice of dolomite slag replenishment technology on large face of converter // Naihuo Cailiao/Refractories. 2020. Vol. 54. No. 3. P. 243–245. https://doi.org/10.3969/j.issn.1001-1935.2020.03.014
12. Kumar D.S., Prasad G., Wishwanath S.C., Ghorui P.K., Mazumdar D., Ranjan M., Lal J.P.N. Converter life enhancement through optimization of operation practices // Ironmaking and Steelmaking. 2007. Vol. 34. No. 6. P. 521–528. https://doi.org/10.1179/174328107X203903
13. Баланин Б.А., Зеленков О.С., Капустин Е.А., Куземко Р.Д. Исследование присоединенной массы сверхзвуковой струи на газодинамическом участке. В кн.: Тепломассообменные процессы в ваннах сталеплавильных агрегатов. Москва: Металлургия, 1975. С. 19–35.
14. Капустин Е.А., Куземко Р.Д., Кузнецов А.Ф., Шам П.И., Большаков В.А. Возможности повышения производительности действующих кислородных конвертеров // Сталь. 1972. № 2. С. 112–115.
15. Tiedje N.S. Solidification, processing and properties of ductile cast iron // Materials Science and Technology. 2010. Vol. 26. No. 5. P. 505–514. https://doi.org/10.1179/026708310X12668415533649
16. Chatterjee A. On some aspects of supersonic jets of interest in LD steelmaking. I. Jet design and characteristics // Iron and Steel. 1976. Vol. 45. No. 69. P. 627–634.
17. Tabata Y., Marsh R.S., Kelly P., etc. Improvement of BOP steel refining blowing control using wide angle lance nozzles. In book: Steel Making Conference Proceedings. 1998. P. 451–457.
18. Явойский В.И., Дорофеев Г.А., Повх И.Л. Теория продувки сталеплавильной ванны. Москва: Металлургия, 1974. 495 с.
19. Протопопов Е.В., Чернятевич А.Г. Исследование взаимодействия кислородных струй с отходящими конвертерными газами // Известия вузов. Черная металлургия. 1996. № 10. С. 5–9.
20. Сизов А.М. Газодинамика и теплообмен газовых струй в металлургических процессах. Москва: Металлургия, 1987. 256 с.
21. Вурцбах Р. Характеристика свободных струй, истекающих из дутьевых сопел // Черные металлы. 1967. № 10. С. 12–20.
22. Kapner J.D., Li K., Larson R.H. An experimental study of mixing phenomena of turbulent supersonic jets // International Journal of Heat and Mass Transfer. 1970. Vol. 13. No. 5. P. 932–937. https://doi.org/10.1016/0017-9310(70)90138-9
23. Sharma S.K., Hlinka J.W., Kern D.W. The bath circulation jet penetration and high – temperature reaction zone in BOF steelmaking // Steelmaking Proceedings. 1977. Vol. 60. P. 181–197.
24. Явойский В.И., Явойский А.В., Сизов А.М. Применение пульсирующего дутья при производстве стали. Москва: Металлургия, 1985. 176 с.
25. Баптизманский В.И., Меджибожский М.Я., Охотский В.Б. Конвертерные процессы производства стали. Киев-Донецк: Вища школа, 1984. 344 с.
Об авторах
Е. В. ПротопоповРоссия
Евгений Валентинович Протопопов, д.т.н., профессор, профессор кафедры металлургии черных металлов
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Л. В. Думова
Россия
Любовь Валерьевна Думова, соискатель степени к.т.н. кафедры металлургии черных металлов
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Н. А. Чернышева
Россия
Наталья Анатольевна Чернышева, доцент кафедры металлургии черных металлов
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
И. В. Ноздрин
Россия
Игорь Викторович Ноздрин, д.т.н., доцент, профессор кафедры металлургии цветных металлов и химической технологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
С. О. Сафонов
Россия
Сергей Олегович Сафонов, аспирант кафедры металлургии черных металлов
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Протопопов Е.В., Думова Л.В., Чернышева Н.А., Ноздрин И.В., Сафонов С.О. Моделирование термогазодинамических параметров нейтральных газовых струй при распространении в полости конвертера. Известия высших учебных заведений. Черная Металлургия. 2022;65(12):843-850. https://doi.org/10.17073/0368-0797-2022-12-843-850
For citation:
Protopopov E.V., Dumova L.V., Nozdrin I.V., Chernysheva N.A., Safonov S.O. Modeling of thermogasodynamic parameters of neutral gas jets when spreading in converter cavity. Izvestiya. Ferrous Metallurgy. 2022;65(12):843-850. (In Russ.) https://doi.org/10.17073/0368-0797-2022-12-843-850