Localization of strains at the initial stage of plastic yield of high manganese steel

Introduction

Certain elements in understanding the nature of strain localization can be associated with autowave ideas of plasticity [1, 2]. It has been demonstrated in [3 – 6] that strain processes in materials are concentrated in strain localization centers, which spontaneously form an ordered evolving strain structure. This structure exists in the form of autowaves of localized plastic yield, and the pattern is a projection of autowaves onto the surface of the strained specimen [1].

In plasticity physics, monocrystals are traditionally used in experimental studies of the main laws and features of plastic strain [7]. The absence of grain bounda­ries therein and the constancy of properties throughout their volume allow for the most accurate representation of the basic elements of glide crystallography. They highlight the stages of the process and relating them to the features of the defect structure and its evolution [8]. Comparative tests performed on monocrystals with different crystal lattices also enable fundamental differences in glide crystallography and strain harde­ning laws to be determined, which are typical of crystals belonging to diffe­rent syngonies.

In this study, data on localized plasticity patterns for alloy Fe – 13 % Mn – 1.03 % C was obtained. The use of monocrystals of high-manganese (13 % Mn) austenitic steels (Hadfield steel [9, 10]) relates to the fact that the choice of orientation of the tensile axis in such monocrystals allows a change in the strain mechanism from dislocation glide to twinning [11, 12]. In this case, loca­lized strain patterns can be compared for different strain mechanisms.

Research materials and methods

The experiments were carried out on monocrystal specimens of high-manganese austenitic steel Fe – 13 % Mn – 1.03 % C. They were homogenized in inert gas at 1373 K and then quenched in water after being held for 1 h at the same temperature of 1373 K. The samples of the following orientations were studied: \([\bar{3}77]\), \([\bar{3}55]\), \([\bar{1}11]\), \([012]\), \([\bar{1}23]\), and work plane indices \((011)\). Hadfield steel with different carbon atom content has a FCC structure. It does not undergo martensitic transformation, and is strained by glide and mechanical twinning in a wide temperature range (T = 233 ÷ 573 K) with a high strain-hardening coefficient [13 – 15]. The cause of strong strain-hardening is usually attributed to the development of mechanical twinning [16 – 20]. An effective mechanism of hardening is the intersection of twins formed in several systems simultaneously [9, 10]. From the very beginning of the plastic yield at T ≈ 300 K, in contrast to low-strength FCC pure metals and alloys, in Hadfield steel crystals there is the twinning in orientations for which the Schmid twinning/glide ratio is 1. This means that carbon atom hardening has a greater resistance to glide dislocation movement than twinning. In Hadfield steel monocrystals, the following factors depend on the orientation of the crystal tensile axis [11, 12]: the type of yield curves; the strain hardening coefficient; the duration of hardening stages; and the mechanical characte­ristics.

Room temperature uniaxial tension mechanical tests at a rate of 1.2·10^–4 s^–1 of flat specimens 30×5×1.5 mm were combined with registration and analysis of the localized plasticity pattern, as in [3 – 6], beginning from the yield point at a frequency of 15 s (every 0.2 % of the total strain). The method of registration and interpretation of specklegrams, based on the use of double-exposed speckle photography, enables the field of displacement vectors to be reconstructed. Thus the components of the plastic distortion tensor can be calculated thus significantly enriching the information on the plastic yield. The details and capacities of the method are described in [1]. The microstructure of the studied monocrystals was investigated in detail in [11, 12].

Research results

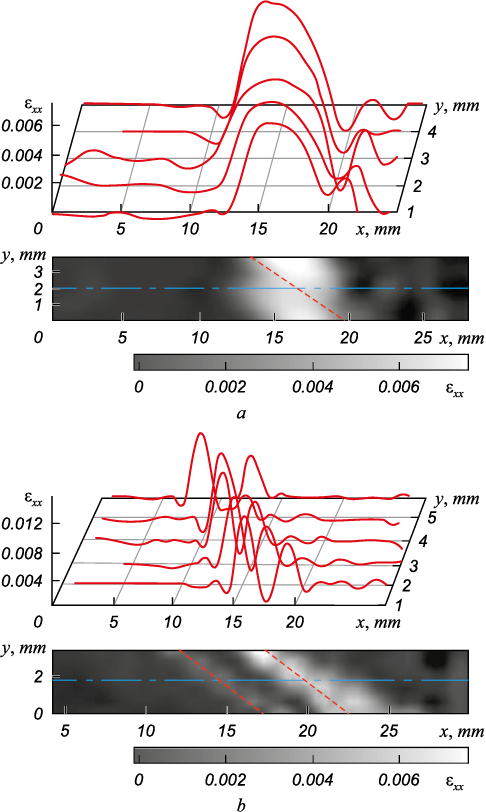
In Hadfield steel monocrystals oriented along direction \([\bar{3}77]\), the existence of a “tooth” and a yield point are related to nucleation and propagation along the crystal of the Lüders band consisting of strain twins in the primary twinning system \([\bar{2}11](111)\) with the maximum Schmid factor of m₁ = 0.5. Metallographic analysis of twinning traces on the work surface of such specimens at stage I (yield point) shows that they are inclined to the specimen axis at an angle of φ = 35°. The pattern of local elongation ε_xx distributions at stage I represents a moving single zone of localized strains (Fig. 1, a). The data presented in Fig. 1, a as a map, where the light regions corres­pond to large values of ε_xx, shows that this localized zone is inclined to the longitudinal axis of the specimen at an angle of φ = 40 ± 5°, as can be determined from the coordinates of ε_xx maximums. This is due to the action of the primary twinning system, traces of which, as indicated above, are inclined to axis \([\bar{3}77]\) at an angle of φ = 35°.

The strain localization pattern in monocrystals orien­ted along direction \([\bar{3}55]\) at the yield point was similar to that described above for the tensile axis \([\bar{3}77]\) orientation. It also represented a moving single strain front of the localized strain. The orientation \([\bar{3}55]\) is in the standard stereographic triangle between two ultimate cases \([\bar{1}11]\) and \([\bar{3}77]\). Thus the strain curve of such specimens contains, in addition to the yield point (stage I), a stage with a small but non-zero strain hardening coefficient which corresponds to the stage of easy glide during dislocation strain. At this stage, separation of localized strain centers was observed. As can be seen (Fig. 1, b), another front of localized plasticity separates from the primary strain center (a halftone map of local elongation distributions is presented, where light areas correspond to major ε_xx values). Two zones of strain localization are seen to be inclined to the longitudinal axis of the specimen at an angle of φ = 40 ± 5°, determined by the maximum coordinates of ε_xx (Fig. 1, b). This is caused by the action of predominant twinning system \([\bar{2}11]\)\((111)\), the traces from which are inclined to axis [55] at an angle of φ = 35°.

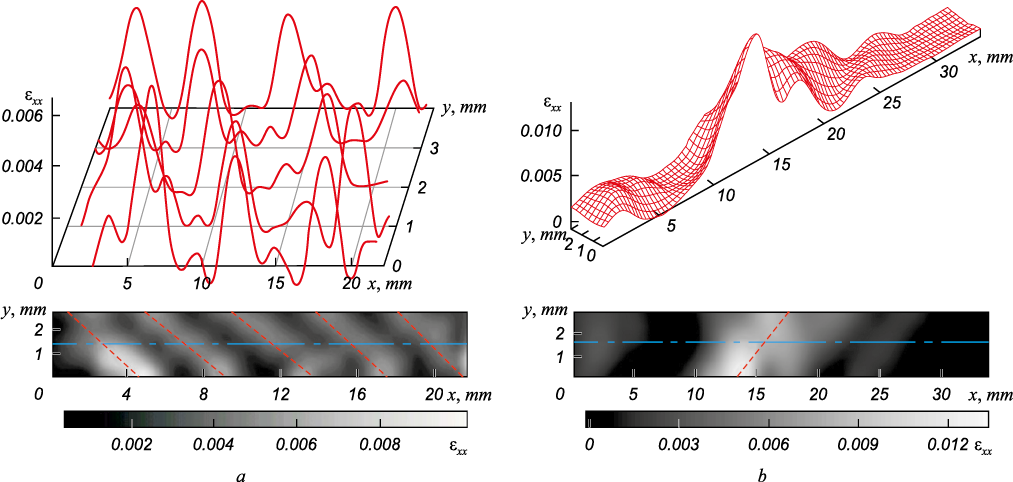
In monocrystals oriented along direction \([\bar{1}11]\), the strain deformation occurs mainly due to one twinning system \([\bar{2}11]\)\((111)\) with the maximum Schmid factor of m₁ = 0.314. Metallographic analysis of twinning traces on the work surface of specimens showed that they were inclined to the specimen axis at an angle of φ = 25°. Distri­butions of local elongations at the easy glide stage of these monocrystals was a set of four broad strain zones located at equal distances, moving synchronously along the specimen. Fig. 2, a shows the distribution of longitudinal component ε_xx along the pattern of the Hadfield steel monocrystal, typical for linear harde­ning stage. This distribution is a set of strain localization zones located at distances of 5.0 ± 1 mm. Fig. 2, a halftone map (where the light areas correspond to major ε_xx values) demonstrates that these areas are inclined to the longitudinal axis of the specimen in the same manner as at the easy glide stage. The angles of inclination of these zones towards the tensile axis, determined from the ε_xx maximum coordinates (Fig. 2, a), are φ = 20 ± 5°. This is clearly caused by the action of twinning system \([\bar{2}11]\)\((111)\), traces of which, as indicated above, are inclined towards axis \([\bar{1}11]\) at an angle of φ = 25°. In monocrystals oriented along directions \([\bar{3}77]\) and \([\bar{3}55]\), a similar strain localization pattern was observed at line­ar hardening stages in the form of a set of five strain localization zones located at distances of 5.0 ± 1 mm.

In monocrystals oriented along direction  \([012]\), a high Schmid factor (~0.49) corresponds to two glide systems: \([\bar{1}01]\) \((111)\) and  \([\bar{1}0\bar{1}]\) \((\bar{1}11)\). Glide traces on the work surface of the specimen under the action of these systems should be inclined towards the tensile direction at angles of 51 and 161°. Optical microscopy revealed traces of active glide system \([\bar{1}01]\) \((111)\) at the easy glide stage, inclined towards the specimen axis at an angle of 47°. Fig. 2, b shows the distribution of longitudinal component ε_xx over the specimen with the axis orientation along \([012]\), characteristic of the easy glide stage. This represents a moving wide single zone of localized strain, consisting of two connected centers. Fig. 2, b shows a halftone map of local strain distributions for the case, where the light area corresponds to major values of ε_xx. This zone is inclined towards the longitudinal axis of the specimen at an angle of φ = 50 ± 5°. This fact is clearly caused by the action of primary glide system \([\bar{1}01]\) \((111)\), the traces of which, as indicated above, are inclined to the axis at an angle of φ₁= 47°.

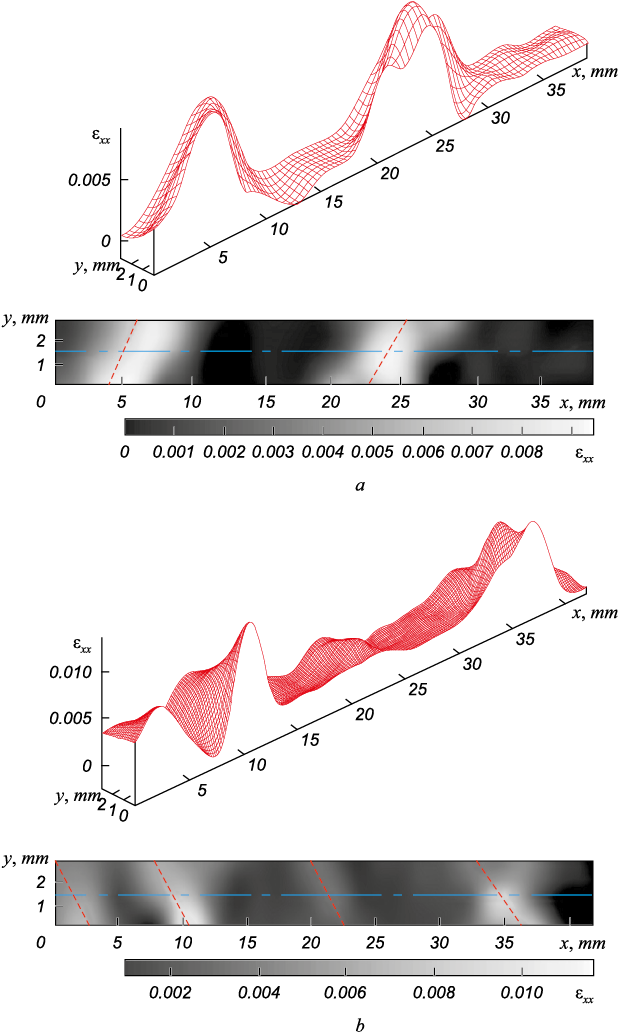
For monocrystals with tensile axis \([\bar{1}23]\), dislocation glide also takes place in the same system \([\bar{1}01]\) \((111)\) from the beginning of yield. In a metallographic thin section, glide traces therein form an angle of 65° with the specimen axis.

The strain macrolocalization pattern at the easy glide stage represented two moving broad strain zones (Fig. 3, a). The halftone map of local elongation ε_xx distri­bution (Fig. 3, a) shows that these localized strain zones are inclined towards the longitudinal axis of the specimen at an angle of φ = 60 ± 5°, caused by the action of primary glide system \([\bar{1}01]\) \((111)\). Further strain of these crystals caused a change in the active strain mechanism from dislocation glide towards twinning at the linear hardening stage. The hardening of crystals in this case is due to the development of twinning firstly in one and then in several systems. The strain localization pattern at the stage of linear hardening is the movement of four localized strain zones at equal (6.0 ± 1 mm) distances (Fig. 3, b). In the halftone map of localized strain distributions for this case, the light areas correspond to major values of ε_xx. The four zones can be seen to be inclined towards the longitudinal axis of the specimen at an angle of φ = 120 ± 5° (Fig. 3, b). At these strain stages, it is difficult to identify the predominant glide or twinning system and relate the incline of the centers to it.

It can be assumed that the inclination angle of locali­zation zones is set by acting twinning system \([\bar{2}11]\) \((111)\). This is also the case for the strain of monocrystal specimens with orientations of tensile axes \([\bar{1}11]\) and \([\bar{3}77]\), in which predominant development of twinning is observed at the linear hardening stage.

Studies of plastic strain localization at the easy glide stage revealed significant differences in the nature of plastic strain macrolocalization in the monocrystal specimens under study. All strain localization patterns observed in these cases can be divided into two types. The first type of strain localization corresponds to the nucleation at the upper yield point and to further propagation of the strain front which gradually transforms the specimen material from an undeformed state to a deformed one. In the second type of localization a synchronous movement of several strain centers occurs in the specimen at the easy glide stage. Their movement may be unidirectional or counteracting, and their velocities may be either the same or different. The number of active glide or twinning systems in the tensile strain of monocrystals studied on the basis of the crystallographic analysis and metallographic studies can be considered as a reason for the difference between the two types of macrostrain localization at stage I (easy glide and yield point). 

 Conclusion

Patterns of localized strain of high-manganese steel monocrystals were studied by means of speckle photography. It was established that the spatial orientation of macroscopic localized strain zones with respect to the tensile axis of a monocrystal specimen is determined by crystallographic parameters. This coincides with traces of active glide or twinning systems with maximum valu­es of Schmid factors at the plane of observance of centers. It was demonstrated that each of the active centers of localized plastic strain is a set of displacement and shift vectors acting on glide planes of monocrystals with maximum Schmid factors, or a set of strain twins which also satisfies this condition, at a time correspon­ding to the registration of the fields.

Analysis of local distributions suggests that the number of active centers of localized plastic strain, acting at the easy glide stage of the studied monocrystals, is determined by the number of glide or twinning systems acting at a given crystallographic orientation. In the case of monocrystals oriented for singlet glide, there is only one localized plasticity center. In the case of multiplet glide, two or more centers coexist simultaneously, each of which has an orientation corresponding to one of the activated glide systems.